Diffusie

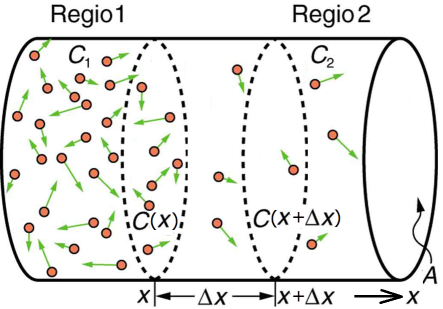
Fysische chemie leert dat er een beweging is van ionen van hoge naar lage concentratie en dat de flux \(\Phi\), d.w.z. de netto verplaatsing van ionen per tijdseenheid per oppervlakte-eenheid in de richting van de afnemende concentratie, gegeven wordt door de wet van Fick: \[\Phi= -D\cdot \frac{\dd C}{\dd x}\] waarbij \(D\) de diffusiecoëfficiënt is en \(\dfrac{\dd C}{\dd x}\) de component van de gradiënt van de concentratie is die wijst in de richting waarin het transport (lokaal) plaatsvindt (in onderstaande tekening de positieve \(x\)-richting). Het minteken verdisconteert dat de richting van het transport er een is van plaatsen met een hoge concentratie naar plaatsen met een lage concentratie. Onderstaande figuur visualiseert dit proces en de formule \[\Phi(x)\cdot \Delta x \approx -D\cdot \bigl(C(x+\Delta x)-C(x)\bigr)\] symboliseert dat het aantal deeltjes dat het volume tussen \(x\) en \(x+\Delta x\) per tijdseenheid instroomt evenredig is met het concentratieverschil op plek \(x\) en \(x+\Delta x\) op dat tijdstip.

Einstein en Nernst hebben de volgende formule voor de diffusieconstante van een geladen deeltje afgeleid: \[D=\frac{RT}{F}\cdot u\] waarbij \(R\) de gasconstante is, \(T\) de absolute temperatuur (in Kelvin), \(F\) de constante van Faraday (de lading van een mol eenwaardige ionen) en \(u\) de 'mobiliteit' van het ion. Wanneer één mol ionen met valentie \(z\) (het aantal ladingseenheden per ion) diffundeert kunnen we dit interpreteren als een elektrische stroom met stroomsterkte \[I_D= zF\cdot \Phi = - zRT\cdot u\cdot \frac{\dd C}{\dd x} \]

Beweging van ionen in een elektrisch veld

Door de diffusiebeweging van ionen in een regio met hoge concentratie naar een regio met lage concentratie, die van elkaar gescheiden zijn door een semipermeabel membraan, ontstaat een ladingsverschil ter plaatse van het membraan. Stel dat het ion positief geladen is, een hoge concentratie binnen de cel heeft, en een lage concentratie buiten de cel heeft, dan zal er door de diffusiebeweging aan de binnenkant in de buurt van het membraan een negatieve lading achterblijven en aan de buitenkant in de buurt van het membraan een positieve lading ontstaan. Het membraan is op deze manier een condensator en naarmate er meer ionen diffunderen zal het ladingsverschil toenemen. Maar dit betekent ook dat er een toenemend potentiaalverschil in de buurt van het membraan ontstaat. Het diffunderen van de ionen zal hierdoor steeds moelijker gaan vanwege tegenwerkende elektrische krachten. De flux \(\Phi_E\) ten gevolge van het elektrisch veld \(E\) dat bij het potentiaalverschil \(V\) past wordt gegeven door de volgende formule: \[\Phi_E=-z\cdot u\cdot C\cdot \frac{\dd V}{\dd x}\] waarbij \(z\) weer de valentie van het ion is en \(\dfrac{\dd V}{\dd x}\) het potentiaalverschil per afstand is. Wanneer één mol deeltjes met valentie \(z\) beweegt in het elektrisch veld kunnen we dit interpreteren als een elektrische stroom met stroomsterkte \[I_E=zF\cdot\Phi_E = -z^2F\cdot u\cdot C\cdot \frac{\dd V}{\dd x}\]

De Nernstvergelijking

Er ontstaat van lieverlee een evenwichtssituatie waarin de diffusiebeweging en de beweging van de ionen in een elektrisch veld even groot, maar tegengesteld gericht zijn; we zeggen wel dat de cel 'in rust' is, maar er is wel beweging van ionen door het membraan waarbij de in- en uitstroom gelijk aan elkaar is. Anders geformuleerd: in evenwicht is de som van de elektrische stroom door diffusie en de beweging in een elektrisch veld, \(I_D+I_E\), gelijk aan nul. Dus: \[I_D+I_E = -z\cdot u\cdot \!\!\left(RT\cdot \frac{\dd C}{\dd x}+zFC\cdot \frac{\dd V}{\dd x}\right)=0\] In evenwicht moet dus de term tussen haakjes gelijk zijn aan nul, en er geldt dan: \[-\frac{RT}{zF}\cdot \frac{1}{C}\cdot \frac{\dd C}{\dd x}= \frac{\dd V}{\dd x}\] Dit impliceert \[-\frac{RT}{zF}\cdot \frac{\dd\ln(C)}{\dd x}= \frac{\dd V}{\dd x}\] en daarom krijgen we bij integratie over de lipide dubbellaag en toepassing van de rekenregel \(\ln(x)-\ln(y)=\ln(x/y)\) de vergelijking \[-\frac{RT}{zF}\ln\left(\frac{C_\mathrm{e}}{C_\mathrm{i}}\right)=V_\mathrm{e}-V_\mathrm{i}\] Dus: \[V_\mathrm{i}-V_\mathrm{e}=\frac{RT}{zF}\ln\left(\frac{C_\mathrm{e}}{C_\mathrm{i}}\right)=\] Het gaat aan de linkerkant om een potentiaalverschil tussen binnen- en buitenkant van het membraan voor een cel in rust, maar in elektrofysiologie is het gebruikelijk om de referentiepotentiaal aan de buitenkant van de cel ter plaatse van het membraan gelijk op nul te stellen. Bij een positief geladen ion met een hogere concentratie aan de binnenkant van de cel in rust zal de potentiaal dan aan de binnenkant van de cel ter plaatse van het membraan een negatieve waarde hebben die we de Nernstpotentiaal of evenwichtspotentiaal van het ion noemen en aanduiden met \(E_\mathrm{ion}\). De gevonden vergelijking heet de wet van Nernst.