Bioelectricity: Electric model of the cell membrane
 An electrical analogue of a single ion species and ion channel
An electrical analogue of a single ion species and ion channel
Electrical analogue of an ion channel
The previous description of the functioning of an ion channel and the cell membrane as a capacitor matches the analogue of an electrical circuit in which each ion channel corresponds to a battery and resistor in series, which are connected together in turn in parallel with a capacitor. Sometimes you see the battery omitted in bioelectrical descriptions of a cell, as if only semipermeability of the membrane is important for the ion and the cell is passive and at rest. But the ion concentration gradient also plays a major role in membrane voltage: because this gradient can vary and in this way change voltage, this can be better considered as a battery in the analogue of an electrical circuit.
Each ion channel thus corresponds to a battery and resistor in series, as visualized in the figure below.
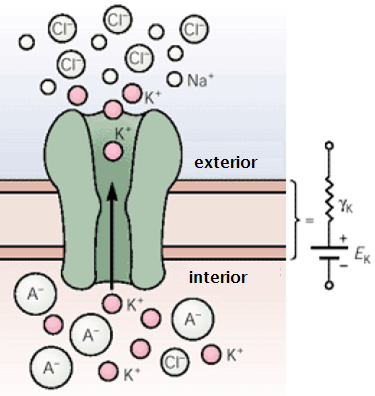
The entire functioning of the ion channel and cell membrane is then represented by an electrical circuit as shown in the figure below. Here, \(E_\mathrm{K}\) is the Nernst potential of the ion channel on the basis of differences in concentration inside and outside the cell. Convention in the electrophysiology is to choose the flow direction of positively charged particles from the inside to the outside of the cell. In a picture (below for the \(\mathrm{K}^{+}\) ion, but usually we drop the charge symbol and symbolize only the name of the ion), the electric circuit looks as follows:
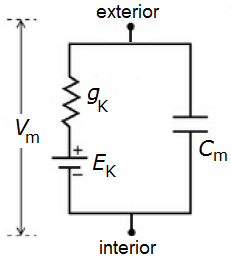
The specific capacitance \(C_\mathrm{m}\) of the membrane (also referred to as capacitance density) depends on the thickness of the lipid bilayer, but it is generally in the order of 1 uF/cm2. The membrane potential \(V_m\) is defined as \(V_i-V_e\) because of the choice of the direction of current. Because the ion channels in the membrane are arranged in parallel, the replacement conductivity equals the sum of the conductivities of individual channels; \(g_\mathrm{K}\) is therefore the product of the number of ion channels per unit area and the conductivity of a single ion channel. Also in this case we are actully talking about specific conductivity (also called conductivity density).
At rest it follows in the above situation from Kirchhoff's loop rule for voltage that \(V_m\) is equal to the Nernst potential \(E_\mathrm{K}\), and this is then the resting membrane potential. In the presence of more ionic channels, the resting membrane potential \(V_r\) can be approximated by a weighted average of the Nernst potentials of the involved ion channels.
units
The unit of the specific capacitance of the cell membrane is uF/cm2. The unit of specific conductivity of ion channels is mS/cm2. The unit for the specific current through the cell membrane (current density) is uA/cm2. But in textbooks and in exercises you also encounter units without "per square centimetre". What has been assumed in this case is that a fixed chosen surface area of the cell membrane is used in calculations. For example, you can take the circular cross-section of an electrode. With an area of \(\pi\cdot 17.84\cdot 17.84\,\text{µm}^{3}\) (think of a circular area with a diameter of 17.84 microns3) you will get, for example, the same numerical value of the current, but now in the unit nA.
In these course notes we will often omit the adjective "specific". We write, for example, "conductivity" instead of "specific conductivity". You can see via the listed units (e.g. \(\text{µA}/\text{cm}^2\) ) what is exactly meant. When misunderstandings could arise, our wording is more precise.
The (specific) electrophysiological quantities usually refer to a piece of an axon or dendrite of a certain unit length and a piece of membrane with a certain unit surface area. In the following table we have listed the most commonly used units in neurophysiology and that of corresponding specific quantities.
\[\begin{array}{|l|l|l|} \hline \mathit{Quantity} & \mathit{Unit} & \textit{Description}\\ \hline a & \text{µm} & \text{radius of a cylindric axon}\\ \hline r_m & \Omega\;\text{cm} & \text{membrane resistance (per inverse unit length)}\\ & & (1/\text{conductivity per unit length}) \\ \hline r_a & \Omega/\text{cm} & \text{axial resistance (per unit length)}\\ \hline c_m & \text{µF}/\text{cm} & \text{membrane capacitance (per unit length)}\\ \hline R_m =r_m\cdot 2\pi a & \Omega\;\text{cm}^2 & \text{specific membrane resistance}\\ & & (1/\text{specific membrane resistance per unit area}) \\ \hline R_a =r_a\cdot \pi a^2& \Omega\;\text{cm} & \text{specific axial resistance (per cross section)}\\ \hline C_m=c_m/(2\pi a) & \text{µF}/\text{cm}^2 & \text{specific membrane capacitance (per unit area)} \\ \hline V_m & \text{mV} & \text{membrane potential}\\ \hline V_r & \text{mV} & \text{resting membrane potential}\\ \hline i_m & \text{µA}/\text{cm} & \text{membrane current (per unit length)} \\ \hline i_a & \text{µA} & \text{axial current}\\ \hline I_m=i_m/(2\pi a) & \text{µA}/\text{cm}^2 & \text{current density of the membrane}\\ \hline I_a=i_a/(\pi a^2) & \text{µA}/\text{cm}^2 & \text{specific axial current (per cross section)}\\ \hline\end{array}\]
Re-establishment of the equilibrium when a stimulus stops
At rest it follows from Kirchhoff's junction rule for current that for an imposed current \(I_\mathrm{stim}\), also called injected current, is equal to the sum of the currents through the ion channel and the capacitor; together with Ohm's law we get: \[\begin{aligned}I_\mathrm{stim}&=I_\mathrm{C_m} + I_\mathrm{K} \\ &= C_m\frac{\dd V_m}{\dd t} + g_\mathrm{\small K} (V_m-E_\mathrm{K})\\ &= C_m\frac{\dd(V_m-E_\mathrm{K})}{\dd t} + g_\mathrm{\small K} (V_m-E_\mathrm{K})\end{aligned}\] When we define \(V=V_m-E_\mathrm{K}\), that is consider the potential difference of the membrane potentiona; with the Nernst potential, we get the following differential equation for the membrane potential \[I_\mathrm{stim}=C_m\frac{\dd V}{\dd t} + g_\mathrm{\small K} V\] When the stimulus is equal to zero, then the differential equation is the same as the differential equation of a discharging capacitor. In a cell that is not at rest, but has, for example, a nonzero starting value of the voltage \(V_0\) at time \(t=0\), the voltage will approach the original potential via an exponential decay process with the formula \[V(t)=V_0\cdot e^{-\frac{ g_\mathrm{\small K}}{C_m}t}\]
Towards a new equilibrium after the start of a stimulus
Now suppose that the membrane potential in our model is equal to the Nernst potential, that is ( \(V=0\)), and that at some moment, say at time \(t=0\), a stimulus is imposed that leads to a constant current \(I_\mathrm{stim}\). Then we have the following initial value problem \[C_m\cdot \frac{\dd V}{\dd t} +g_K\cdot V= I, \quad V(0)=0\] Thus: \[ \frac{\dd V}{\dd t}=\frac{I_\mathrm{stim}}{C_m}-\frac{g_K}{C_m}\cdot V, \quad V(0)=0\] This is a differential equation of limited exponential growth and its solution is \[V(t)= \frac{I_\mathrm{stim}}{g_K}\cdot \left(1-e^{-\frac{g}{C_m}\cdot t}\right)\] Thus, the voltage approaches a nonzero equilibrium value, that is, the membrane voltage is adjusted to a new value after some time. There will also briefly exist a current through the circuit by the charging and discharging of the capacitor (depending on the stimulus).
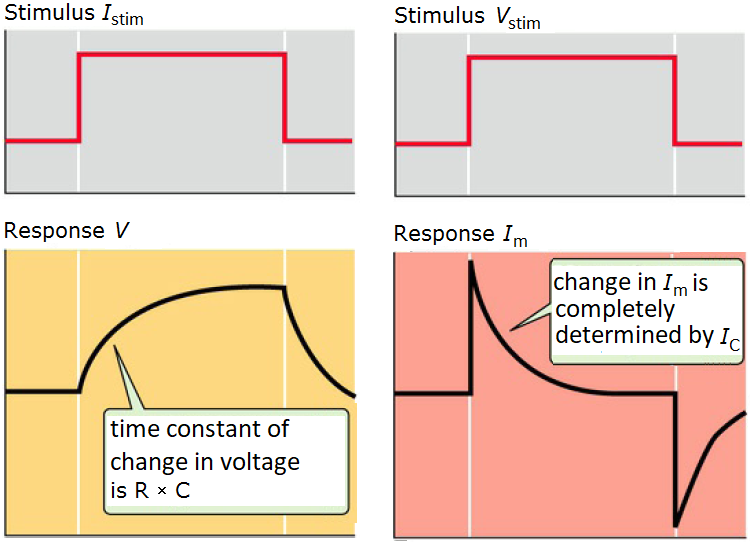
Visual summary
The following picture shows the response of the membrane potential and membrane current, respectively, to a short rectangular current stimulus and voltage stimulus, respectively.