Bioelektriciteit: Elektrisch model van het celmembraan
 Een elektrisch analogon voor één ionsoort en ionkanaal
Een elektrisch analogon voor één ionsoort en ionkanaal
Elektrisch analogon voor een ionkanaal
Bij de eerdere beschrijving van de werking van een ionkanaal en het celmembraan als condensator past het analogon van een elektrisch circuit waarin elk ionkanaal correspondeert met een in serie geschakelde batterij en weerstand, die samen op hun beurt parallel geschakeld zijn met een condensator. Soms zie je in bio-elektrische beschrijvingen van een cel de batterij weggelaten, alsof alleen de semipermeabiliteit van het membraan voor het ion belangrijk is en de cel passief en in rust is. Maar de ionconcentratiegradiënt speelt ook een grote rol in membraanspanning: omdat deze gradiënt kan variëren kan dit in het analogon van een elektrisch circuit beter als batterij beschouwd worden.
Elk ionkanaal correspondeert dus met een in serie geschakelde batterij en weerstand, zoals in onderstaande figuur gevisualiseerd wordt.
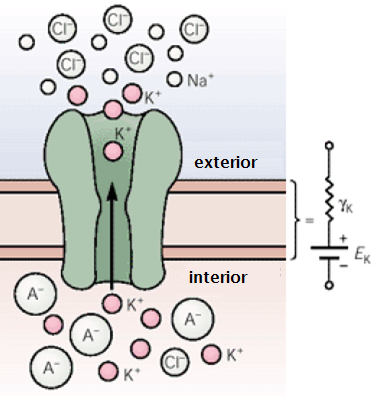
De hele werking van ionkanaal en celmembraan wordt dan gerepresenteerd door een elektrisch circuit zoals in onderstaande figuur. Hierin is \(E_\mathrm{K}\) de Nernstpotentiaal van het ionkanaal op basis van concentratieverschillen binnen en buiten de cel. Conventie in de elektrofysiologie is hierbij om de stroomrichting van positief geladen deeltjes van binnen naar buiten de cel te kiezen. In een plaatje (hier voor het \(\mathrm{K}^{+}\) ion, maar meestal laten we de lading weg en symboliseren alleen de naam van het ion) ziet het elektrische circuit er als volgt uit:
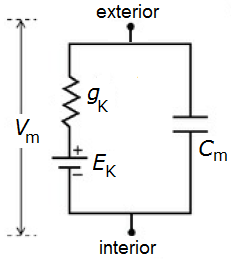
De specifieke capaciteit \(C_\mathrm{m}\) van het membraan (ook de capaciteitsdichtheid genoemd) hangt af van de dikte van de lipide dubbellaag, maar is in het algemeen in de orde van 1 #\mathrm{µ}#F/cm2. De membraanpotentiaal \(V_m\) is hierbij gelijkgesteld aan \(V_i-V_e\) vanwege de keuze van de stroomrichting. Omdat de ionkanalen in het membraan parallel geschakeld zijn is de vervangingsgeleidbaarheid de som van de geleidbaarheden van individuele kanalen; \(g_\mathrm{K}\) is dus het product van het aantal ionkanalen per oppervlakte-eenheid en de geleidbaarheid van een enkel ionkanaal. Ook hier hebben we het eigenlijk over specifieke geleidbaarheid (ook wel geleidbaarheidsdichtheid genoemd).
In rust volgt in bovenstaande situatie uit de spanningswet van Kirchhoff dat \(V_m\) gelijk is aan de Nernstpotentiaal \(E_\mathrm{K}\) en dit wordt dan de rustmembraanpotentiaal. Bij aanwezigheid van meer ionkanalen kan de rustmembraanpotentiaal \(V_r\) benaderd worden als een gewogen gemiddeldevan de Nernstpotentialen van de bijpassende ionkanalen.
Eenheden
De eenheid van de specifieke capaciteit van het celmembraan is #\mathrm{µ}#F/cm2. De eenheid van specifieke geleidbaarheid voor ionkanalen is mS/cm2. De eenheid voor de specifieke stroomsterkte in het celmembraan (stroomdichtheid) is #\mathrm{µ}#A/cm2. Maar in leerboeken en opgaven kom je deze eenheden ook tegen zonder "per vierkante centimeter". Wat men dan gedaan heeft is een vastgekozen oppervlak van het celmembraan te gebruiken in berekeningen. Bijvoorbeeld kun je de cirkelvormige dwarsdoorsnede van een elektrode nemen. Bij een oppervlakte van \(\pi\cdot 17.84\cdot 17.84\,\mathrm{µ}\text{m}^{3}\) (denk aan een cirkelvormig gebied met diameter 17.84 #\mathrm{µ}#m3) krijg je dan bijvoorbeeld eenzelfde getalswaarde voor de stroomsterkte, maar dan in de eenheid nA.
In dit dictaat zullen we vaak het bijvoeglijke naamwoord "specifiek" weglaten. We schrijven dan bijvoorbeeld "geleidbaarheid" i.p.v. "specifieke geleidbaarheid". Aan de vermelde eenheden (bijvoorbeeld \(\mathrm{µ}\text{A}/\text{cm}^2\)) kan je al aflezen wat precies bedoeld is. Wanneer er misverstand kan ontstaan, dan zijn we in de woordkeuze preciezer.
De (specifieke) elektrofysiologische grootheden hebben dus meestal betrekking op een stukje axon of dendriet van zekere eenheidslengte en een stukje membraan met een zekere eenheidsoppervlakte. In onderstaande tabel staan de meest gebruikte eenheden in neurofysiologie en die van bijpassende specifieke grootheden.
\[\begin{array}{|l|l|l|} \hline \mathit{Grootheid} & \mathit{Eenheid} & \textit{Beschrijving}\\ \hline a & \mathrm{µ}\text{m} & \text{straal van een cylindrisch axon}\\ \hline r_m & \Omega\;\text{cm} & \text{membraanweerstand (per inverse eenheidslengte)}\\ & & (1/\text{geleidbaarheid per eenheidslengte}) \\ \hline r_a & \Omega/\text{cm} & \text{axiale weerstand (per eenheidslengte)}\\ \hline c_m & \mathrm{µ}\text{F}/\text{cm} & \text{membraancapaciteit (per eenheidslengte)}\\ \hline R_m =r_m\cdot 2\pi a & \Omega\;\text{cm}^2 & \text{specifieke membraanweerstand}\\ & & (1/\text{specifieke geleidbaarheid per eenheidsoppervlakte}) \\ \hline R_a =r_a\cdot \pi a^2& \Omega\;\text{cm} & \text{specifieke axiale weerstand (per dwarsdoorsnede)}\\ \hline C_m=c_m/(2\pi a) & \mathrm{µ}\text{F}/\text{cm}^2 & \text{specifieke membraancapaciteit (per eenheidsoppervlakte)} \\ \hline V_m & \text{mV} & \text{membraanpotentiaal}\\ \hline V_r & \text{mV} & \text{rustmembraanpotentiaal}\\ \hline i_m & \mathrm{µ}\text{A}/\text{cm} & \text{membraanstroomsterkte (per eenheidslengte)} \\ \hline i_a & \mathrm{µ}\text{A} & \text{axiale stroomsterkte}\\ \hline I_m=i_m/(2\pi a) & \mathrm{µ}\text{A}/\text{cm}^2 & \text{stroomdichtheid van het membraan}\\ \hline I_a=i_a/(\pi a^2) & \mathrm{µ}\text{A}/\text{cm}^2 & \text{specifieke axiale stroomsterkte (per dwarsdoorsnede)}\\ \hline\end{array}\]
Herstel van evenwicht als een stimulus stopt
Uit de stroomwet van Kirchhoff volgt dan dat voor een opgelegde stroom \(I_\mathrm{stim}\), ook wel geïnjecteerde stroom genaamd, geldt dat dit gelijk is aan de som van de stromen van het ionkanaal en de condensator; samen met de wet van Ohm geeft dit: \[\begin{aligned}I_\mathrm{stim}&=I_\mathrm{C_m} + I_\mathrm{K} \\ &= C_m\frac{\dd V_m}{\dd t} + g_\mathrm{\small K} (V_m-E_\mathrm{K})\\ &= C_m\frac{\dd(V_m-E_\mathrm{K})}{\dd t} + g_\mathrm{\small K} (V_m-E_\mathrm{K})\end{aligned}\] Als we \(V=V_m-E_\mathrm{K}\) definiëren, dat wil zeggen kijken naar het potentiaalverschil met de Nernstpotentiaal, dan krijgen we de volgende differentiaalvergelijking voor de membraanpotentiaal \[I_\mathrm{stim}=C_m\frac{\dd V}{\dd t} + g_\mathrm{\small K} V\] Als de stimulus gelijk aan nul, dan is de differentiaalvergelijking dezelfde als die van een ontladende condensator. Bij een cel die niet in rust is, maar bijvoorbeeld een startwaarde van de spanning \(V_0\) ongelijk aan nul heeft op tijdstip \(t=0\), zal de spanning de oorspronkelijke potentiaal naderen via een exponentieel verval proces volgens de formule \[V(t)=V_0\cdot e^{-\frac{ g_\mathrm{\small K}}{C_m}t}\]
Naar een nieuw evenwicht na de start van een stimulus
Stel nu eens dat in ons model de membraanpotentiaal gelijk is aan de Nernstpotentiaal, dat wil zeggen (\(V=0\)), en dat op zeker moment, het tijdstip \(t=0\) gesteld, een stimulus opgelegd wordt die een constante stroomsterkte \(I_\mathrm{stim}\) tot gevolg heeft. Dan hebben we te maken met het volgende beginwaardenprobleem \[C_m\cdot \frac{\dd V}{\dd t} +g_K\cdot V= I, \quad V(0)=0\] oftewel \[ \frac{\dd V}{\dd t}=\frac{I_\mathrm{stim}}{C_m}-\frac{g_K}{C_m}\cdot V, \quad V(0)=0\] Dit is een differentiaalvergelijking van begrensde exponentiële groei en de oplossing is \[V(t)= \frac{I_\mathrm{stim}}{g_K}\cdot \left(1-e^{-\frac{g}{C_m}\cdot t}\right)\] De spanning nadert dus een evenwichtswaarde ongelijk aan nul, dat wil zeggen dat de membraanspanning na zekere tijd zich instelt op een nieuwe waarde. Er zal ook kortstondig een stroom door het circuit gaan door op- of ontlading van de condensator (afhankelijk van de stimulus).
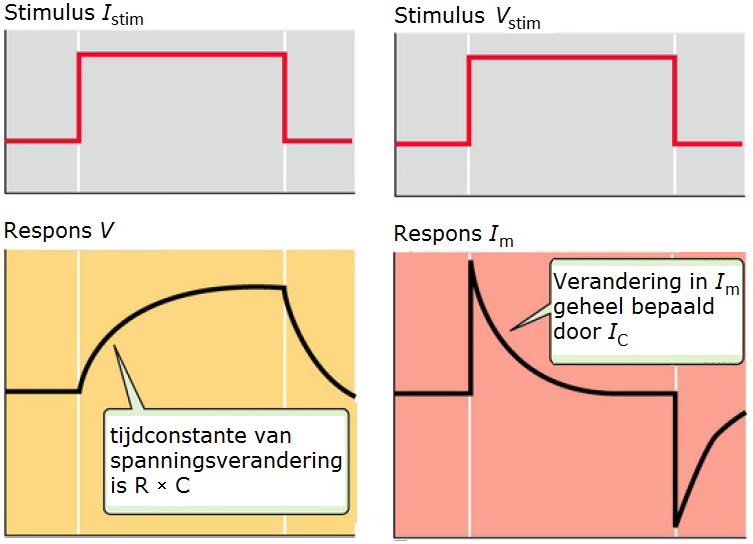
Visuele samenvatting
Het volgende plaatje geeft de respons van de membraanspanning respectievelijk de membraanstroom op een kortstondige rechthoekige stroomstimulus respectievelijk spanningstimulus.