Bioelectricity: Electric model of the cell membrane
 Membrane potential for two ion species and ion channels
Membrane potential for two ion species and ion channels
In the real physiological situation we are dealing with more than one ion species and more than one type of ion channel. How can we describe an equilibrium in this case? We explain this for two ion species, each with its own ion channel and for convenience we take two ions playing an important role in cell regularisation, namely the potassium and sodium ion (\(\mathrm{K}^{+}\) and \(\mathrm{Na}^{+}\)). We consider the situation inside and outside the cell at a temperature of \(29.25\,{}^{\circ}\mathrm{C}\) as illustrated in the figure below.
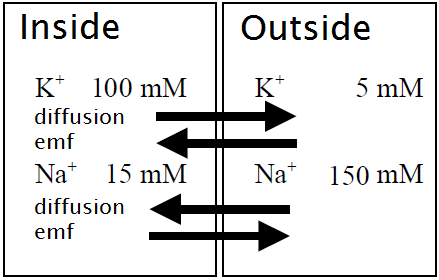
For the two ion species, the diffusion forces and electric field forces are again the main factors that come into play. The Nernst potential of an ion at the given temperature can be calculated by the formula \[E_\mathrm{ion} =-\frac{60}{z}\cdot \log_{10}\left(\frac{C_\mathrm{i}}{C_\mathrm{e}}\right)\] In this case, the equilibrium for potassium ions is at an electric potential \(E_{\mathrm{K}^{+}}\) of \({}-78\,\mathrm{mV}\) and the equilibrium for sodium ions is at an electric potential \(E_{\mathrm{Na}^{+}}\) of \({}+60\,\mathrm{mV}\) (calculation after!). The real membrane potential \(V_m\) will lie somewhere inbetween. But where? We will see that it is a weighted average of the two Nernst potentials formula and, for reasons that will later be revealed, call it the linearized GHK equation. For simplicity, we will denote quantities like \(E_{\mathrm{Na}}\), \(E_{\mathrm{K}}\), etc., because formulas are less readable when we add the valencies of the ions.
The linearized GHK equation for two ion channels The linearized GHK equation for two ion channels, say potassium and sodium channels, allows you to compute the resting membrane potential \(V_m\): \[V_m=\frac{g_\mathrm{K}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{K} + \frac{g_\mathrm{Na}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{Na}\]
The derivation of the linearized GHK-equation for two ion channels is relatively simple. When no current is injected, Kirchhoff's junction rule for current gives: \[I_\mathrm{K}+I_\mathrm{Na}+I_{\mathrm{C_m}}=0\] For the ionic currents we have according to Ohm's law \[\begin{aligned}I_\mathrm{K}\,&=g_\mathrm{K}(V_m-E_\mathrm{K}) \\ I_\mathrm{Na}\,&=g_\mathrm{Na}(V_m-E_\mathrm{Na})\end{aligned}\] where \(g_\mathrm{K}\) and \(g_\mathrm{Na}\) are the conductivity of the potassium and sodium channel, respectively. For the cell membrane as a capacitor, the relationship between current and voltage is \[I_{\mathrm{C_m}}=C_m\frac{dV_m}{dt}\] At rest, the membrane voltage is constant, and the derivative thereof must be equal to zero. This implies \[I_\mathrm{K}+I_\mathrm{Na} = g_\mathrm{K}(V_m-E_\mathrm{K}) + g_\mathrm{Na}(V_m-E_\mathrm{Na})=0\] This equation can be rewritten as (check this!) \[\begin{aligned} V_m&=\frac{g_\mathrm{K}E_\mathrm{K}+g_\mathrm{Na}E_\mathrm{Na}}{g_\mathrm{K}+g_\mathrm{Na}}\\ \\ &=\frac{g_\mathrm{K}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{K} + \frac{g_\mathrm{Na}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{Na}\end{aligned}\] This equation can also be written as \[V_m=\lambda\cdot E_\mathrm{K}+(1-\lambda)\cdot E_\mathrm{Na}\] with \[0\le \lambda = \frac{g_\mathrm{K}}{g_\mathrm{K}+g_\mathrm{Na}}\le 1\]
So the final equilibrium potential or resting membrane potential is always a weighted average of the Nernst potentials of the two ion species, and the weights depend upon the conductivities of the two ionic species. For example, if the conductivity of the sodium ion channel is equal to zero, then the resting membrane potential is equal to the Nernst potential of the potassium ion. Conversely, if the conductivity of the potassium ion channel is equal to zero, then the resting membrane potential equal to the Nernst potential of the sodium ion. In practice, the conductivity of the potassium ion channel will be greater than that of the sodium ion channel and the resting membrane potential will be slightly above that of the Nernst potential of the potassium ion. The result is that there is a small flow of potassium ions from inside to outside the cell with an equally large but opposite flow of sodium ions from outside to inside the cell. These currents are so small that they have no major effect on the ion concentrations.
Sodium-potassium pump
In the long term, the sodium-potassium pump must actively exchange sodium ions with potassium ions to restore the equilibrium state. This pump exchanges 3 sodium ions for 2 potassium ions per cycle and decreases the membrane potential, which would otherwise increase in the long term to a value near zero. Watch the animation explaining functioning of the sodium-potassium pump (click on the video tab)
Animation of the sodium-potassium pump (in Dutch, taken from Jeroen Alessie, Avans)
Let us do claculation about the situation shown in the picture with the following information: \[
\begin{array}{l|rrrr}
\mathrm{ion\;} X & [X]_\mathrm{e} & [X]_\mathrm{i} & g_X\;(\mathrm{mS/cm}^2) & E_X\;(\mathrm{mV})\\ \hline
\mathrm{K}^{+} & 5 & 100 & 100 & {}-78 \\
\mathrm{Na}^{+} & 150 & 15 & 10 & {}+60
\end{array}\] The resting membrane potential \(V_m\) can be computed as follows: \[V_m=\frac{100\times -78+ 10\times 60}{100+10}\approx -65.5\,\mathrm{mV}\] You see: it is above the Nernst potential for potassium, but closer to this electric potential than the Nernst potential of sodium because the cell is less permeable to this ion species.


