Bioelektriciteit: Elektrisch model van het celmembraan
 Membraanpotentiaal bij twee ionsoorten en ionkanalen
Membraanpotentiaal bij twee ionsoorten en ionkanalen
In de echte fysiologische situatie hebben we te maken met meer dan één ionsoort en meer dan één type ionkanaal. Hoe kunnen we dan een situatie van evenwicht beschrijven? We leggen dit uit voor twee ionsoorten met elk hun eigen ionkanaal en voor het gemak nemen we twee ionen die een belangrijke rol in celregularisatie spelen, namelijk het kaliumion en het natriumion (\(\mathrm{K}^{+}\) en \(\mathrm{Na}^{+}\)). We bekijken de in onderstaande figuur gegeven toestand binnen en buiten de cel bij een temperatuur van \(29.2\,{}^{\circ}\mathrm{C}\).
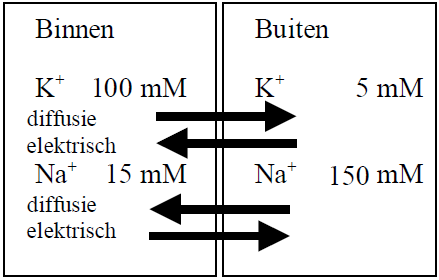
Voor de twee ionsoorten zijn de diffusiekrachten en elektrische krachten weer de belangrijkste factoren. De Nernstpotentiaal van een ion kan bij de gegeven temperatuur berekend worden met de formule \[E_\mathrm{ion} =-\frac{60}{z}\cdot \log_{10}\left(\frac{C_\mathrm{i}}{C_\mathrm{e}}\right)\] In dit geval ligt het evenwicht voor kaliumionen bij een potentiaal \(E_{\mathrm{K}^{+}}\) van \({}-78\,\mathrm{mV}\) en ligt het evenwicht voor natriumionen bij een potentiaal \(E_{\mathrm{Na}^{+}}\) van \({}+60\,\mathrm{mV}\) (reken na!). De echte membraanspanning \(V_m\) zal hier ergens tussenin liggen. Maar waar? We zullen zien dat het een gewogen gemiddelde van de twee Nernstpotentialen is en de formule zullen we om redenen die later uit de doeken gedaan worden de gelineariseerde GHK-vergelijking noemen. Voor de eenvoud zullen we de notatie \(E_{\mathrm{Na}}\), \(E_{\mathrm{K}}\), enzovoorts, hanteren want door de valenties erbij te schrijven worden de formules niet leesbaarder.
De gelineariseerde GHK-vergelijking bij twee ionkanalen De gelineariseerde GHK-vergelijking bij twee ionkanalen, zeg bij kalium- en natriumkanalen, stelt je in staat om de rustmembraanpotentiaal \(V_m\) te berekenen: \[V_m=\frac{g_\mathrm{K}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{K} + \frac{g_\mathrm{Na}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{Na}\]
De afleiding van de gelineariseerde GHK-vergelijking bij twee ionkanalen is betrekkelijk eenvoudig. Wanneer er geen stroom geïnjecteerd wordt, volgt uit de stroomwet van Kirchhoff: \[I_\mathrm{K}+I_\mathrm{Na}+I_{\mathrm{C_m}}=0\] Voor de ionstromen geldt volgens de wet van Ohm \[\begin{aligned}I_\mathrm{K}\,&=g_\mathrm{K}(V_m-E_\mathrm{K}) \\ I_\mathrm{Na}\,&=g_\mathrm{Na}(V_m-E_\mathrm{Na})\end{aligned}\] waarbij \(g_\mathrm{K}\) respectievelijk \(g_\mathrm{Na}\) de geleidbaarheid van het kalium- respectievelijk natriumkanaal is. Voor het celmembraan als condensator is het verband tussen stroomsterkte en spanning \[I_{\mathrm{C_m}}=C_m\frac{dV_m}{dt}\] In rusttoestand is de membraanspanning constant en de afgeleide hiervan dus gelijk aan nul. Dientengevolge geldt dan \[I_\mathrm{K}+I_\mathrm{Na} = g_\mathrm{K}(V_m-E_\mathrm{K}) + g_\mathrm{Na}(V_m-E_\mathrm{Na})=0\] Deze gelijkheid kun je herleiden tot (ga dit na!) \[\begin{aligned} V_m&=\frac{g_\mathrm{K}E_\mathrm{K}+g_\mathrm{Na}E_\mathrm{Na}}{g_\mathrm{K}+g_\mathrm{Na}}\\ \\ &=\frac{g_\mathrm{K}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{K} + \frac{g_\mathrm{Na}}{g_\mathrm{K}+g_\mathrm{Na}}\cdot E_\mathrm{Na}\end{aligned}\] Deze gelijkheid kun je ook opschrijven als \[V_m=\lambda\cdot E_\mathrm{K}+(1-\lambda)\cdot E_\mathrm{Na}\] met \[0\le \lambda = \frac{g_\mathrm{K}}{g_\mathrm{K}+g_\mathrm{Na}}\le 1\]
De uiteindelijke evenwichtspotentiaal of rustmembraanpotentiaal is dus altijd een gewogen gemiddelde van de Nernstpotentialen van de twee ionsoorten en deze weging hangt af van de geleidbaarheid van de beide ionsoorten. Als bijvoorbeeld de geleidbaarheid van het natriumionkanaal gelijk aan nul is, dan is de rustmembraanpotentiaal gelijk aan de Nernstpotentiaal van het kaliumion. Omgekeerd, als de geleidbaarheid van het kaliumionkanaal gelijk aan nul is, dan is de rustmembraanpotentiaal gelijk aan de Nernstpotentiaal van het natriumion. In praktijk zal de geleidbaarheid van het kaliumionkanaal groter zijn dan die van het natriumionkanaal en zal de rustmembraanpotentiaal een klein beetje boven die van de Nernstpotentiaal van het kaliumion liggen. Het gevolg is dat er een kleine stroom van kaliumionen van binnen naar buiten de cel is met een even grote maar tegengestelde stroom van natriumionen van buiten naar binnen de cel. Deze stromen zijn zo klein dat ze geen grote gevolgen hebben voor de ionconcentraties.
Natrium-kalium pomp
Op lange termijn moet voor herstel van evenwicht wel de natrium-kalium pomp actief natriumionen omwisselen met kaliumionen. Deze pomp wisselt 3 natriumionen voor 2 kaliumionen om per cyclus en verlaagt de membraanpotentiaal daar waar ze anders op termijn zou gaan stijgen en naar een waarde dicht bij nul zou gaan. Bekijk de animatie met uitleg over werking van de natrium-kalium pomp (klik op de video-tab)
Animatie over natrium-kalium pomp (afkomstig van Jeroen Alessie, Avans Hogeschool)
Laten we de in het plaatje getekende situatie eens doorrekenen met de volgende gegevens: \[
\begin{array}{l|rrrr}
\mathrm{ion\;} X & [X]_\mathrm{e} & [X]_\mathrm{i} & g_X\;(\mathrm{mS/cm}^2) & E_X\;(\mathrm{mV})\\ \hline
\mathrm{K}^{+} & 5 & 100 & 100 & {}-78 \\
\mathrm{Na}^{+} & 150 & 15 & 10 & {}+60
\end{array}\] De rustmembraanpotentiaal \(V_m\) is dan als volgt te berekenen: \[V_m=\frac{100\times -78+ 10\times 60}{100+10}\approx -65.5\,\mathrm{mV}\] Je ziet het: hoger dan de Nernstpotentiaal van kalium, maar wel dichter bij deze spanning dan bij de Nernstpotentiaal van natrium omdat de cel minder doorlaatbaar is voor deze ionsoort.


