The model for two ion channels can be extended to three or more ion channels. For convenience, we summarize below the other ion channels by a single so-called "leakage channel" having conductivity \(g_\mathrm{L}\). Then we have an analogue of an electrical circuit that looks as follows:

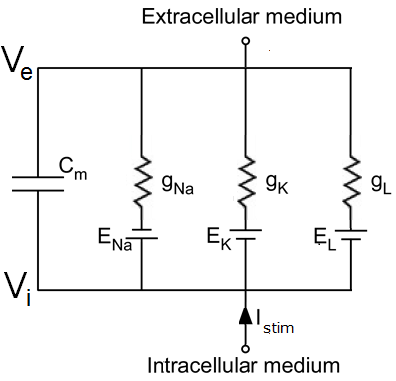
In this figure, we have also drawn an imposed current, \(I_\mathrm{stim}\). The membrane potentental is defined as \(V_m=V_i-V_e\)

From Kirchhoff's junction rule it follows that the imposed current \(I_\mathrm{stim}\) is equal to the sum of the currents of the ion channels and the capacitor; along with Ohm's law this leads to: \[\begin{aligned}I_\mathrm{stim}&=I_{\mathrm{C_m}} + I_\mathrm{K}+I_\mathrm{Na}+I_\mathrm{L} \\ &= C_m\frac{dV_m}{dt} + g_\mathrm{\small K} (V_m-E_\mathrm{K})+ g_\mathrm{\small Na} (V_m-E_\mathrm{Na})+ g_\mathrm{\small L} (V_m-E_\mathrm{L})\end{aligned}\] If we define the resting membrane potential \(V_r\) define as \[V_\mathrm{r} = \frac{g_\mathrm{\small K} E_\mathrm{K}+ g_\mathrm{\small Na}E_\mathrm{Na}+ g_\mathrm{\small L}E_\mathrm{L}}{g_\mathrm{\small K} + g_\mathrm{\small Na}+ g_\mathrm{\small L}}\] and define \[V=V_m-V_r\], when we consider the potential difference with the resting membrane potential, then we get the following differential equation (check!) \[I_\mathrm{stim}=C_m\frac{dV}{dt} + (g_\mathrm{\small K} + g_\mathrm{\small Na}+ g_\mathrm{\small L}) V\] If the stimulus is equal to zero, then the differential equation is the same as that of a discharging capacitor. In a cell that is not at rest, but has, for example, a bonzero starting value of the voltage \(V\) at time \(t=0\), the voltage will approach the original potential via an exponential decay process, according to the formula \[V(t)=V(0)\cdot e^{-\frac{g_m}{C_m}t}\] where \(g_m\) is equal to the sum of the conductitivities of the ion channels.

\(\phantom{x}\)

In reality, the situation is even more complicated. For the channel conductivity \(g_{\mathrm{ion}}\) one often takes the product of a maximum channel conductivity \(G_{\mathrm{ion}}\) and the chance \(p\) that the ion channels are open and ion transport possible; this probability depends in many models on the potential and time. We will see this when we discuss the Hodgkin-Huxley model for action potentials in nerve cells.