Metingen van Hodgkin en Huxley in voltage-clamp experimenten

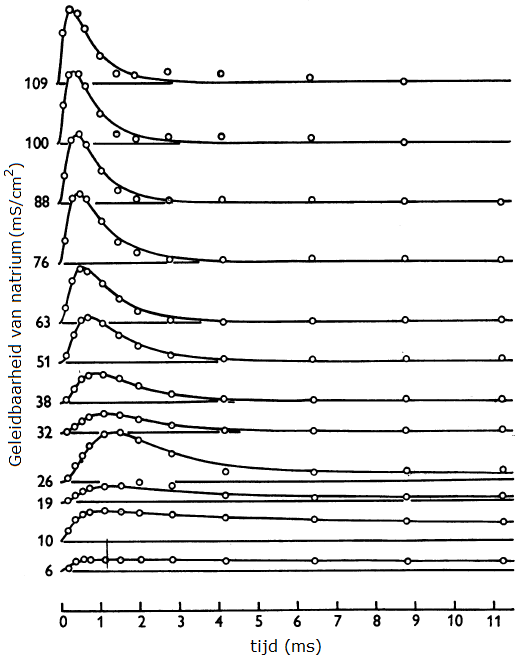
Onderstaand diagram toont de meetpunten van Hodgkin en Huxley van hun voltage-clamp experimenten waarin de geleidbaarheid van natriumkanalen bij verschillende opgelegde spanningen in de loop van de tijd is uitgezet. Bedenk dat het hier steeds stapsgewijze verhogingen van de opgelegde spanning (rechts bij de krommen genoteerd) gaat en de reactie van het membraan hierop betreft. Voor de geleidbaarheid $g_\mathrm{Na}$ geldt:

$$g_\mathrm{Na}=\frac{V_m-E_\mathrm{Na}}{I_\mathrm{Na}}$$ oftewel $$I_\mathrm{Na}=g_\mathrm{Na}(V_m-E_\mathrm{Na})$$ De meetgegevens bij een opgelegde spanning zijn vervolgens steeds gemodelleerd met een wiskundige formule waarvan de grafiek getekend is. De grafieken beschrijven de meetgegevens goed.

Normering

De grafiek van de geleidbaarheid $g_\mathrm{Na}$ van natriumkanalen bij toenemende spanning is ingewikkelder dan die bij kalium: nu neemt aanvankelijk de geleidbaarheid toe, maar vervolgens neemt deze weer af, met een maximum dat binnen 1 milliseconde is bereikt. Als je de grafieken normeert dan zijn ze in feite allemaal van dezelfde vorm (zie onderstaand diagram). Normering is in feite niet veel anders dan de geleidbaarheid van $g_\mathrm{Na}$ te schrijven als het product van de maximale geleidbaarheid, zeg $\overline{g_\mathrm{Na}}$ en een functie $p_\mathrm{Na}(t)$:

$$g_\mathrm{Na}=\overline{g_\mathrm{Na}}\cdot p_\mathrm{Na}(t)$$ Deze functie $p_\mathrm{Na}(t)$ is de genormeerde geleidbaarheid van natriumkanalen. Dit stelde Hodgkin en Huxley in staat om een algemene formule voor geleidbaarheid van natriumkanalen als functie van spanning en tijd op te stellen. Maar de fysiologische interpretatie via een poortmechanisme is nu ingewikkelder dan bij het kaliumkanaal, waar per kanaal maar één poorttype met vier identieke componenten verondersteld werd die open of dicht zijn. We veronderstellen nu geen twee maar drie toestanden voor een ionkanaal: open, dicht en geïnactiveerd. Nog steeds spelen vier componenten een rol, maar we onderscheiden nu twee types: de ene voor open/gesloten toestand en de andere voor geïnactiveerd/niet geïnactiveerd.

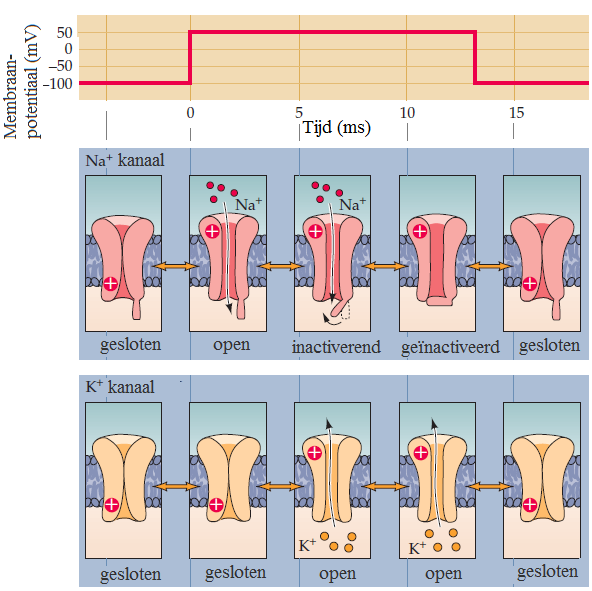
Onderstaande figuur symboliseert de verschillen in toestand van kalium- en natriumkanalen bij een toestand van hyperpolarisatie en depolarisatie. In een toestand van hyperpolarisatie zijn kalium- en natriumkanalen dicht. Bij depolarisatie opent het natriumkanaal zich eerst en pas daarna gaat het kaliumkanaal open. Het kaliumkanaal sluit pas weer als de membraanspanning omlaag gaat. Bij het natriumkanaal gaat dat anders: bij voortdurende depolarisatie raakt het ionkanaal geïnactiveerd (alsof een tweede deur in de gang zich sluit) en kan er toch geen ionenstroom doorheen gaan.

Wiskundig model

Basisidee is weer om eerst een wiskundig model op te stellen waarbij $\overline{g_\mathrm{Na}}$ de maximale geleidbaarheid van natriumkanalen is wanneer alle natriumkanalen open staan en $p_\mathrm{Na}$ de fractie van open natriumkanalen symboliseert. Hodgkin en Huxley veronderstelden dat om stroom door het ionkanaal te kunnen laten stromen drie componenten van een natriumkanaal in de juiste stand moeten zijn, met kans $m(t)$ per component, en één component in de juiste stand moet zijn, met kans $h(t)$, om niet geïnactiveerd te zijn. Opnieuw namen zij aan dat de kansprocessen onafhankelijk zijn. Dit geeft de formule

$$p_\mathrm{Na}=m^3h$$ Naar analogie met chemische reactiekinetiek veronderstelden Hodgkin en Huxley dat er een 'evenwichtsreactie' is van niet-doorlatende naar doorlatende toestand en vice versa met 'reactieconstanten' $\alpha_m$ en $\beta_m$ respectievelijk $\alpha_h$ en $\beta_h$ in een model van elementaire reactievergelijkingen. De indices geven aan met welke component van het ionkanaal we te maken hebben. Net als eerder bij de beschrijving van geleidbaarheid van kaliumkanalen krijgen we differentiaalvergelijkingen van begrensde exponentiële groei. Voor $m(t)$ hebben we $$\frac{\dd m}{\dd t} = \alpha_m(1-m) - \beta_mm$$ met als oplossing onder de veronderstelling dat $m(0)=0$ (kans op doorlaatbare toestand gelijk aan 0): $$m(t) = m_\infty\cdot \left(1-\exp\bigl(-\frac{t}{\tau_m}\bigr)\right)$$ waarbij $$m_\infty = \frac{\alpha_m}{\alpha_m+\beta_m}\quad\mathrm{en}\quad \tau_m=\frac{1}{\alpha_m+\beta_m}$$ Voor $h(t)$ hebben we $$\frac{\dd h}{\dd t} = \alpha_h(1-h) - \beta_hh$$ met als oplossing onder de veronderstelling dat $h(0)=1$ (kans op niet geïnactiveerde toestand gelijk aan 1): $$h(t) = h_\infty\cdot \left(1-\exp\bigl(-\frac{t}{\tau_h}\bigr)\right)+ \exp\bigl(-\frac{t}{\tau_h}\bigr)$$ met $$h_\infty = \frac{\alpha_h}{\alpha_h+\beta_h}\quad\mathrm{en}\quad \tau_m=\frac{1}{\alpha_h+\beta_h}$$

Spanningsafhankelijkheid

Hodgkin en Huxley stelden op basis van hun meetgegevens de volgende formules voor de spanningsafhankelijk parameters voor (in eenheden van $\mathrm{ms}^{-1}$ en $\mathrm{mV}$):

$$\begin{aligned} \alpha_m&= \frac{0.1(25-v)}{\exp\left(\frac{25-v}{10}\right)-1}\\ \\ \beta_m&=4\exp\left(\frac{-v}{18}\right)\\ \\ \alpha_h&=0.07\exp\left(\frac{-v}{20}\right)\\ \\ \beta_h &= \frac{1}{\exp\left(\frac{30-v}{10}\right)+1} \end{aligned}$$ waarbij $v$ het verschil tussen de membraanspanning en de rustmembraanspanning $V_r=-70\;\mathrm{V}$ is. Als je dus de spanningsafhankelijkhied niet ten opzichte van de rustmembraanspanning wilt bestuderen maar ten opzichte van de membraanpotentiaal dan moet je voor $v$ invullen $V-V_r = V+70$.

Wanneer we bovenstaande formules toepassen dan kunnen we de tijdconstanten $\tau_m$ en $\tau_h$ en de steady-state waarden $m_\infty$ en $h_\infty$ uitzetten tegen de spanning $v$ en zo de spanningsafhankelijkheid in grafiekvorm zien:

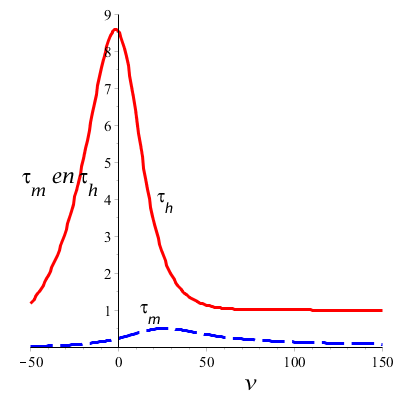
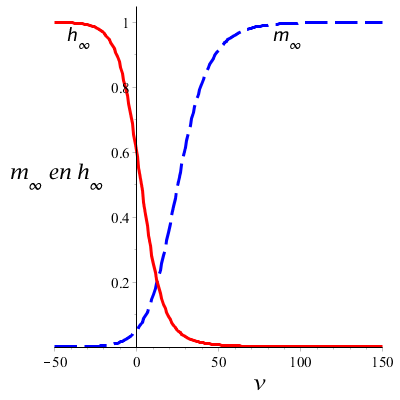
De onderste grafiek laat zien dat bij depolarisatie (positieve $v$) de steady-state waarde $m_\infty$ toeneemt en de steady-state waarde $h_\infty$ afneemt als de spanning groter wordt. Bij hyperpolarisatie (negatieve $v$) is het juist andersom: dan is de steady-state waarde $m_\infty$ klein en de steady-state waarde $h_\infty$ groot. De beide poortmechanismen lijken elkaar als het ware tegen te werken.

De bovenste grafiek laat zien dat de tijdconstante $\tau_h$ een maximum heeft rond de rustpotentiaal en dat de tijdconstante $\tau_h$ een maximum heeft tijdens depolarisatie. Verder valt op dat de tijdconstante $\tau_m$ een stuk kleiner is dan de tijdconstante $\tau_h$, hetgeen suggereert dat dit poortmechanisme sneller reageert op spanningswijzigingen dan het poortmechanisme dat inactivering controleert. Ingeval van depolarisatie neemt de tijdconstante $\tau_h$ af naarmate de spanning groter wordt en deze afname wordt steeds kleiner bij toenemende spanning. Voor de tijdconstante $\tau_m$ is dit anders: eerst zal bij polarisatie de tijdconstante nog toenemen, om vervolgens bij sterkere polarisatie weer af te nemen. Belangrijk is om je te realiseren dat de natriumgeleidbaarheid een samenspel van twee mechanismen is.

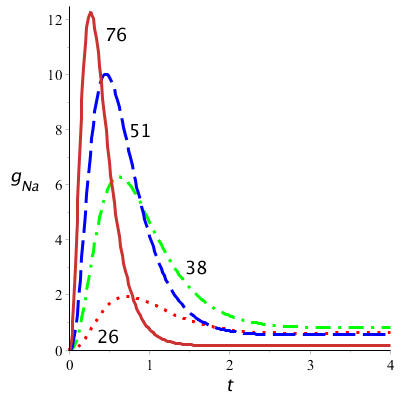
Hieronder zijn grafieken getekend van de modelkrommen van natriumgeleidbaarheid uitgezet tegen tijd voor verschillende waarden van $v$. Hierbij is gebruik gemaakt van de volgende waarde voor de maximale geleidbaarheid: $\overline{g_\mathrm{Na}} =120\;\mathrm{mS\,cm}^{-2}$ en hebben we verondersteld dat $m(0)=0$ en $h(0)=1$. De krommen zien er uit zoals in het eerste diagram van metingen gedaan door Hodgkin en Huxley.