Bioelektriciteit: Actiepotentiaal en het model van Hodgkin en Huxley
 Het model van Hodgkin en Huxley in volle glorie
Het model van Hodgkin en Huxley in volle glorie
We zijn nu zover om het model van Hodgkin en Huxley, toegepast op een reuze-zenuwvezel van een pijlinktvis, in volle glorie te bekijken. We passen het toe op een korte, maar constante stroomstimulus. Het model bestaat uit vier gekoppelde differentiaalvergelijkingen met spanningsafhankelijke parameters die bij de poortmechanismen van kalium- en natriumkanalen horen. Voor de volledigheid worden andere parameters in onderstaand overzicht ook vermeld zodat eenieder de berekeningen kan nadoen met voldoende krachtige wiskundige software. Voor de rustmembraanpotentiaal hebben we \(V_r=-70\;\mathrm{mV}\) genomen.
Modelvergelijkingen van Hodgkin en Huxley
\[\begin{aligned} C_m\frac{\dd V_m}{\dd t} &= -\overline{g_\mathrm{K}}n^4(V_m-E_\mathrm{K})-\overline{g_\mathrm{Na}}m^3h(V_m-E_\mathrm{Na})-\overline{g_\mathrm{L}}(V_m-E_\mathrm{L})+I\\[0.15cm]
\frac{\dd n}{\dd t}&=\alpha_n(V_m)(1-n)-\beta_n(V_m)n\\[0.15cm]
\frac{\dd m}{\dd t}&=\alpha_m(V_m)(1-m)-\beta_m(V_m)m \\[0.15cm]
\frac{\dd h}{\dd t}&=\alpha_h(V_m)(1-h)-\beta_h(V_m)h \\[0.15cm]
\overline{g_\mathrm{K}}&= 36\;\mathrm{mS\,cm}^{-2} \\[0.15cm]
\overline{g_\mathrm{Na}}&= 120\;\mathrm{mS\,cm}^{-2} \\[0.15cm]
\overline{g_\mathrm{L}}&= 0.3\;\mathrm{mS\,cm}^{-2}\\[0.15cm]
E_\mathrm{K}&= -82\;\mathrm{mV} \\[0.15cm]
E_\mathrm{Na}&= 45\;\mathrm{mV} \\[0.15cm]
E_\mathrm{L}&= -59\;\mathrm{mV}\\[0.15cm]
C_m&= 1\,\mathrm{µ}\mathrm{F\,cm}^{-2}\\[0.15cm]
\alpha_n(v) &= \frac{0.01\bigl(10-(v-V_r)\bigr)}{\exp\left(\frac{10-(v-V_r)}{10}\right)-1}\\[0.15cm]
\beta_n(v)&=0.125\exp\left(\frac{-(v-V_r)}{80}\right)\\[0.15cm]
\alpha_m(v)&= \frac{0.1\bigl(25-(v-V_r)\bigr)}{\exp\left(\frac{25-(v-V_r)}{10}\right)-1}\\[0.15cm]
\beta_m(v)&=4\exp\left(\frac{-(v-V_r)}{18}\right)\\[0.15cm]
\alpha_h(v)&=0.07\exp\left(\frac{-(v-V_r)}{20}\right)\\[0.15cm]
\beta_h(v) &= \frac{1}{\exp\left(\frac{30-(v-V_r)}{10}\right)+1}\\[0.15cm]
\end{aligned}\] Als beginwaarden kiezen we \[V_m=V_r=-70\,\mathrm{mV}, n(0)=0.32, m(0)=0.06, h(0)=0.6\] om er voor te zorgen dat de potentiaal zonder stroomtoevoer gelijk blijft. Voor de stroompuls nemen we een rechthoekige puls met verschillende hoogte en duur. Dan kan wiskundige software het beginwaardenprobleem numeriek oplossen en oplossingskrommen tekenen.
Iets overzichtelijker is om de membraanpotentiaal te berekenen t.o.v. de rustmembraanpotentiaal \(V_r\), zeg \(U=V_m-V_r\), en dan tegelijk de Nernstpotentialen t.o.v. de rustmembraanpotentiaal te nemen, zeg \(U_\mathrm{K}=E_\mathrm{K}-V_r\), \(U_\mathrm{Na}=E_\mathrm{Na}-V_r\) en \(U_\mathrm{L}=E_\mathrm{L}-V_r\). Dan wordt het stelsel van differentiaalvergelijkingen \[\begin{aligned} C_m\frac{\dd U}{\dd t} &= -\overline{g_\mathrm{K}}n^4(U-U_\mathrm{K})-\overline{g_\mathrm{Na}}m^3h(U-U_\mathrm{Na})-\overline{g_\mathrm{L}}(U-U_\mathrm{L})+I\\[0.15cm]
\frac{\dd n}{\dd t}&=\alpha_n(U)(1-n)-\beta_n(U)n\\[0.15cm]
\frac{\dd m}{\dd t}&=\alpha_m(U)(1-m)-\beta_m(U)m \\[0.15cm]
\frac{\dd h}{\dd t}&=\alpha_h(U)(1-h)-\beta_h(U)h \\[0.15cm]
\overline{g_\mathrm{K}}&= 36\;\mathrm{mS\,cm}^{-2} \\[0.15cm]
\overline{g_\mathrm{Na}}&= 120\;\mathrm{mS\,cm}^{-2} \\[0.15cm]
\overline{g_\mathrm{L}}&= 0.3\;\mathrm{mS\,cm}^{-2}\\[0.15cm]
E_\mathrm{K}&= -82\;\mathrm{mV} \\[0.15cm]
E_\mathrm{Na}&= 45\;\mathrm{mV} \\[0.15cm]
E_\mathrm{L}&= -59\;\mathrm{mV}\\[0.15cm]
C_m&= 1\,\mathrm{µ}\mathrm{F\,cm}^{-2}\\[0.15cm]
\alpha_n(v) &= \frac{0.01(10-v)}{\exp\left(\frac{10-v}{10}\right)-1}\\[0.15cm]
\beta_n(v)&=0.125\exp\left(\frac{-v}{80}\right)\\[0.15cm]
\alpha_m(v)&= \frac{0.01(25-v)}{\exp\left(\frac{25-v}{10}\right)-1}\\[0.15cm]
\beta_m(v)&=4\exp\left(\frac{-v}{18}\right)\\[0.15cm]
\alpha_h(v)&=0.07\exp\left(\frac{-v}{20}\right)\\[0.15cm]
\beta_h(v) &= \frac{1}{\exp\left(\frac{30-v}{10}\right)+1}\\[0.15cm]
\end{aligned}\] Als beginwaarden kiezen we \[U=0\,\mathrm{mV}, n(0)=0.32, m(0)=0.06, h(0)=0.6\] Wil je daarna de membraanpotentiaal \(V_m\) weten, gebruik dan de relatie \[V_m=U+V_r\tiny.\]
We beginnen een stroompuls die 1 ms duurt, begint op tijdstip \(t=1\;\mathrm{ms}\) en een grootte heeft van 10 #\mathrm{µ}#A/cm2. Dan krijgen we een eenmalige actiepotentiaal en de grafiek van de membraanspanning ziet er als volgt uit:
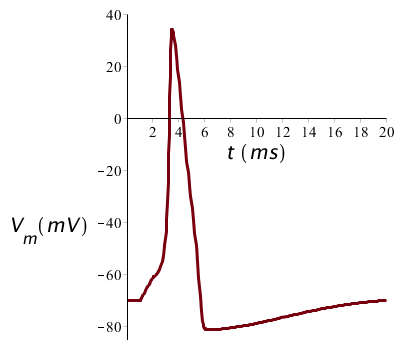
De prikkel moet de membraanpotentiaal wel boven de vuurdrempel brengen anders ontstaat er geen actiepotentiaal. Als we de prikkel in sterkte halveren en dus maar 5 #\mathrm{µ}#A/cm2 stroom toevoegen tijdens 1 ms is wordt de drempel niet bereikt en keert de potentiaal terug naar de rustwaarde zoals in onderstaande figuur te zien is.
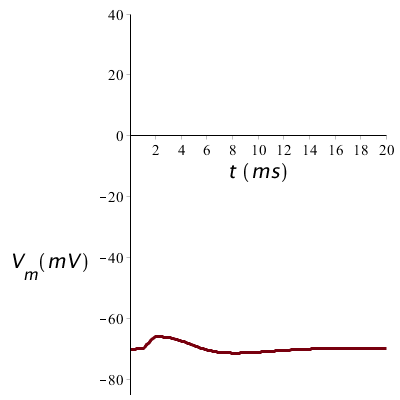
Als de stimulus groot genoeg is om een actiepotentiaal te genereren, dan heeft de daadwerkelijke grootte van de stimulus weinig effect op de vorm van de actiepotentiaal. In onderstaande figuur is het potentiaalverloop bij een twee keer zo grote prikkel (20 #\mathrm{µ}#A/cm2 stroom tijdens 1ms) uitgezet, maar de grafiek ziet er net zo uit als eerst:
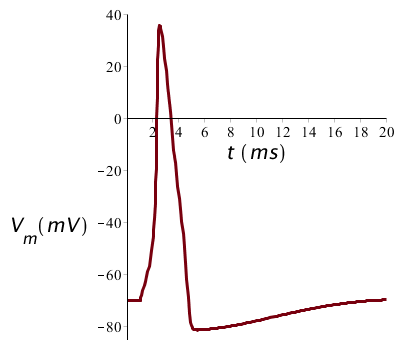
Als de prikkel langdurig is dan kan er een serie van spikes ontstaan: hieronder zie je het potentiaalverloop bij voortdurende stroomtoevoer van 10 mA/cm2:
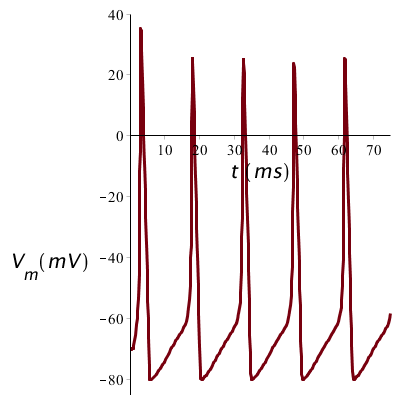
Als de prikkel sterker is, zeg 20 #\mathrm{µ}#A/cm2 in ons rekenvoorbeeld, dan zullen de pieken korter op elkaar liggen, maar verder niet wezenlijk andere vorm hebben. De sterkte van een stimulus vertaalt zich dus in de frequentie van de oscillerende membraan potentiaal.
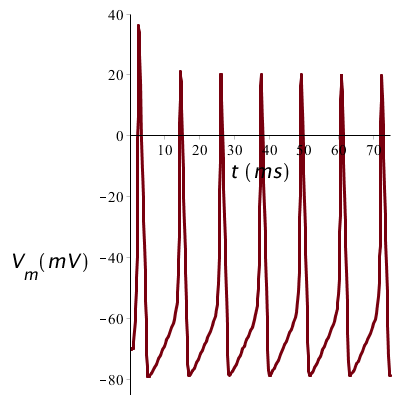
Om de processen die optreden in de kalium- en natriumkanalen tijdens een actiepotentiaal beter te kunnen volgen, helpt het om de grafieken van \(n(t)\), \(m(t)\) en \(h(t)\) te tekenen. Hieronder staan de modelkrommen voor onze eerste situatie van een kortstondige prikkel (10 #\mathrm{µ}#A/cm2 tijdens 1 ms startend op tijdstip \(t=1\;\mathrm{ms}\)).
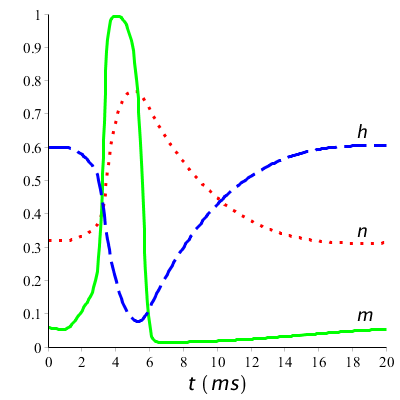
Wat we zien dat is aan het begin van de actiepotentiaal, de waarde van \(m\) omhoog schiet: natriumkanalen openen. Met enige vertraging wordt \(h\) kleiner: natriumkanalen komen in inactieve toestand. Langzaam zal \(h\) weer stijgen: tijdens een zekere periode kan er geen of slecht met moeite een actiepotentiaal teweeg gebracht worden. Ook gaat met vertraging de waarde van \(n\) omlaag: kaliumkanalen openen zich en sluiten weer als de rustpotentiaal dichterbij komt. Bij een langdurige prikkeling met een serie van spikes tot gevolg herhaalt zich dit proces. Hieronder zijn de grafieken getekend bij langdurige prikkeling boven de vuurdrempel.
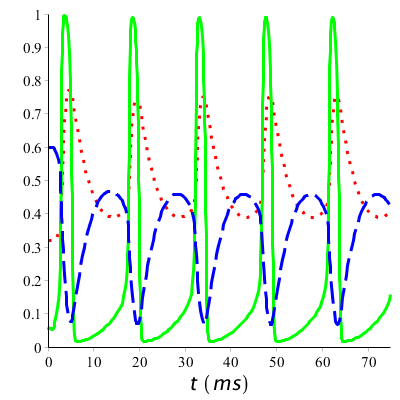
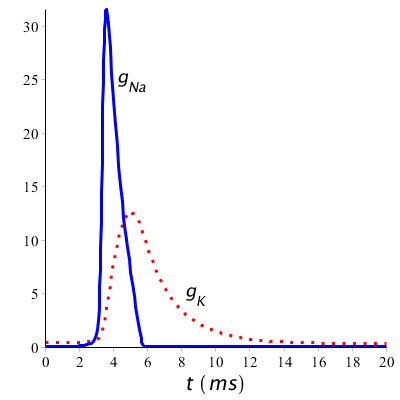
Keren we nog even terug naar de geleidbaarheden van de kalium- en natriumkanalen tijdens een kortstondige prikkeling (met een duur van 1 ms startend op tijdstip 1 ms), dan zien we in onderstaand diagram van de veranderende geleidbaarheden tijdens een actiepotentiaal dat inderdaad eerst de instroom van natriumionen naar de binnenkant van de cel gefaciliteerd wordt, om pas later de uitstroom van kaliumionen gefaciliteerd wordt.