Het model van Hodgkin en Huxley kan in een wiskundige softwareomgeving gesimuleerd worden, bijvoorbeeld in R en RStudio.

Onderstaan R programma simuleert het model voor een kortstondige stimulatie die hoog genoeg is om een actiepotentiaal te bewerkstelligen. Voor overzichtelijkheid wordt hier de verschoven elektrische potentiaal \(U=V-V_r\) met rustmembraanpotentiaal \(V_r\) gemodelleerd en na het oplossen van het stelsel van differentiaalvergelijkingen de membraanpotentiaal \(V=U+V_r\) berekend.

library(deSolve)

model <- function(tijd, begintoestand, parameters) {
  with(as.list(c(begintoestand, parameters)),{
    an <- function(U) 0.01*(10-U)/(exp(1-0.1*U)-1);
    bn <- function(U) 0.125*exp(-0.0125*U);
    am <- function(U) (2.5-0.1*U)/(exp(2.5-0.1*U)-1);
    bm <- function(U) 4*exp(-0.0556*U);
    ah <- function(U) 0.07*exp(-0.05*U);
    bh <- function(U) 1/(exp(3-0.1*U)+1);
    Istim <- function(t, s=start, d=duur) {
      if (t>s && t<s+d) {I} else {0}
    } # stroomstimulus in blokvorm met hoogste waarde I

    dUdt <- (Istim(tijd) - gk*n^4*(U-Uk) - gna*m^3*h*(U-Una) - gl*(U-Ul))/C;
    dndt <- an(U)*(1-n)-bn(U)*n;
    dmdt <- am(U)*(1-m)-bm(U)*m;
    dhdt <- ah(U)*(1-h)-bh(U)*h;

    return(list(c(dUdt, dndt, dmdt, dhdt))) 
  })
}

params <- c(Una=115, Uk=-12, Ul=10.6,
            gna=120, gk=36, gl=0.3, C=1, 
            I=10, start=5, duur=1);

t <- seq(from=0, to=30, by = 0.1);
beginwaarden <- c(U=0, n=0.32, m=0.06, h=0.6);

oplossing <- ode(beginwaarden, t, model, params);
oplossing[,2] <- oplossing[,2] - 70 # V=U+Vrust; Vrust=-70 mV

plot(oplossing, col="blue", lwd=3, 
     xlab="tijd (msec)", ylab=list("V (mV)", "n", "m", "h"),
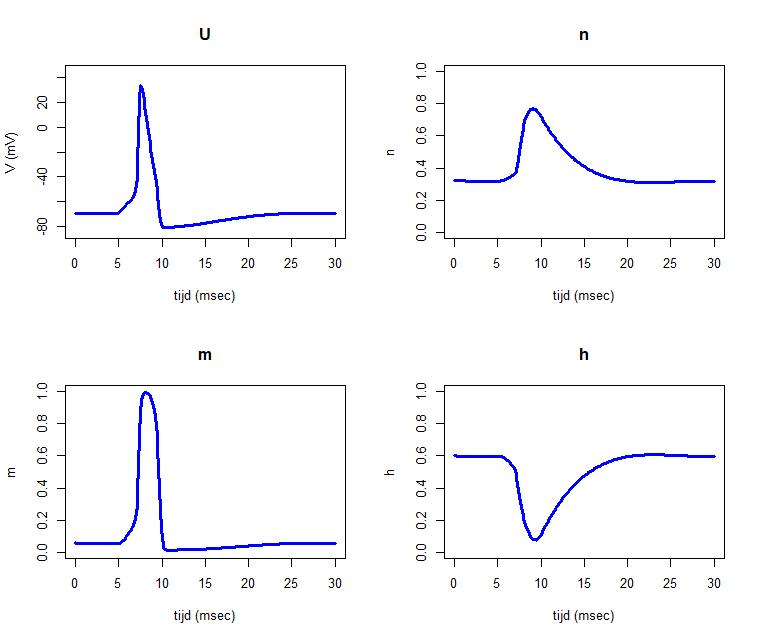
     ylim=list(c(-85,45), c(0,1), c(0,1), c(0,1)))  

Het levert onderstaande diagrammen op.