In a space-clamp experiment, the membrane voltage of a prepared area along the nerve fibre is the same. This means that the spatial organization of a cell is not taken into account. However, this approach is not sustainable for a neuron with a long nerve fibre or a highly branched tree structure of dendrites. To describe the charge propagation along a nerve fibre one uses theory about electrical cables. We will first deal with the passive propagation of electric charge along the cell membrane. This means that the properties of the cell membrane are considered to be constant and does not depend, for example, on the membrane potential. You can think of an experiment in which you change the potential at the beginning of the axon by continuous current injection and then go on until no more changes take place in time (this is called a steady state). The membrane potential will then decrease slowly along the axon because current flow will leak through the membrane. We will set up a mathematical formula for this decrease in membrane potential.
We only discuss a highly simplified model in which
- electrical properties of the cable (for example, membrane capacity, membrane resistance and axial resistance) are the same everywhere;
- the nerve fibre is cylindrical with a constant diameter;
- the extracellular fluid has a negligible resistance (i.e., will be assumed equal to 0 );
- we will work with electric potential with respect to the resting membrane potential to make things easier.
The figure below shows the electrical model of a piece of a cylindrical cable. It shows the electrical properties of the cell membrane with resistance \(r_m\), connected in parallel with the capacitance \(c_m\), and axial resistance \(r_a\) of the intracellular fluid. The membrane is represented as a series of parallel connected resistors and capacitors. \(I_a\) and \(I_m\) are, respectively, the axial current and the membrane current.
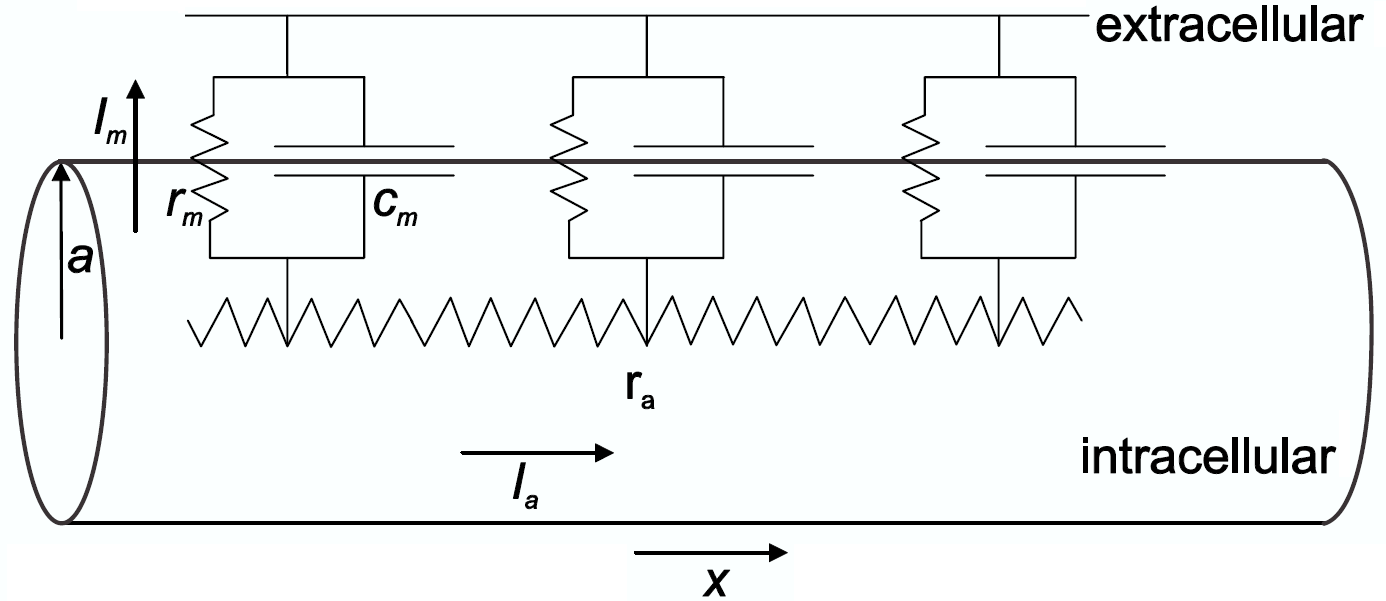
The quantities \(r_m\), \(r_a\) and \(c_m\) are always related to a piece of axon of a certain unit length.
In the table below are listed the corresponding units, specific quantities, and other commonly used electro-physiological quantities. \[\begin{array}{|l|l|l|} \hline \mathit{Quantity} & \mathit{Unit} & \textit{Description}\\ \hline a & \text{µm} & \text{radius of a cylindrical axon}\\ \hline r_m & \Omega\;\text{cm} & \text{membra resistane (per inverse unit of length)}\\ & & (1/\text{conductivity per unit length}) \\ \hline r_a & \Omega/\text{cm} & \text{axial resistance (per unit of length)}\\ \hline c_m & \text{µF}/\text{cm} & \text{membrane capacitance (per unit length)}\\ \hline R_m =r_m\cdot 2\pi a & \Omega\;\text{cm}^2 & \text{specific membrane resistance}\\ & & (1/\text{specific conductivity per unit of area}) \\ \hline R_a =r_a\cdot \pi a^2& \Omega\;\text{cm} & \text{specific axial resistance (per cross section)}\\ \hline C_m=c_m/(2\pi a) & \text{µF}/\text{cm}^2 & \text{specific membrane capacitance (per unit of area)} \\ \hline V_m & \text{mV} & \text{membrane potential}\\ \hline V_r & \text{mV} & \text{resting membrane potential}\\ \hline i_m & \text{µA}/\text{cm} & \text{membrane current flow (per unit of length)} \\ \hline i_a & \text{µA} & \text{axial current flow}\\ \hline I_m=i_m/(2\pi a) & \text{µA}/\text{cm}^2 & \text{current density of the membrane}\\ \hline I_a=i_a/(\pi a^2) & \text{µA}/\text{cm}^2 & \text{specific axial current flow (per cross section)}\\ \hline\end{array}\]
Consider an axon as a chain of successive pieces that
- each consist of a membrane part which is modelled as a parallel circuit of a resistor and a capacitor;
- are connected among themselves with resistors which describe the flow in the axoplasm (we neglect the resistance of the extracellular fluid)
Assume a cylindrical axon with the axis equal to the positive \(x\) axis. Suppose that change the voltage by current injection at time \(t=0\) in \(x=0\) and maintain the voltage by continuous current injection. This current flows through the axon, but there is also leakage flow through the membrane. This means that the voltage \(V\) is not everywhere the same along the axon and also will depend on time; we indicate this by denoting \(V\) explicitly as a function of place and time, say \(V(x,t)\).
This location- and time-dependent potential is the solution of the following partial differential equation, which is referred to as the cable equation, with boundary value \(V(0,t)=V_0\) : \[\lambda^2\cdot \frac{\partial^2 V}{\partial x^2}=\tau_m\cdot \frac{\partial V}{\partial t}+V, \qquad V(0,t)=V_0\] with \[\lambda=\sqrt{\frac{r_m}{r_a}}=\sqrt{\frac{a\cdot R_m}{2R_a}},\quad\tau=r_m\cdot c_m=R_m\cdot C_m\] After a sufficiently long time, the membrane potential along the axon will not change over time. We can then consider the membrane voltage as a function \(V(x)\) and the partial differential equation becomes the following ordinary differential equation \[\lambda^2\cdot \frac{\dd^2V}{\dd x^2}=V, \qquad V(0)=V_0\] The solution to this initial value problem is an exponential decay curve \[V(x)=V(0)\cdot e^{-\frac{x}{\lambda}}\]
For the math enthusiast, we present the derivation of the cable equation.
According to Ohm's law, the axial current \(i_a\) is proportional to the change in potential in the longitudinal direction and can be written as \[i_a=-\frac{1}{r_a}\cdot\frac{\partial V}{\partial x}\] where \(r_a\) is the axial resistance in \(\Omega/\text{cm}\). The minus sign in this equation is there because the current flow is from a high to a low potential. So \(I_a\) is positive when \(\dfrac{\partial V}{\partial x}\) is negative. The symbol \(\partial\) denotes partial differentiation, here in the \(x\) coordinate. We will not go much into this except by stating that the partial derivatives can be defined here as \[\frac{\partial V}{\partial x}=\lim_{h\to 0}\frac{V(x+h,t)-V(x,t)}{h}\] and that one can compute the partial derivative with respect to \(x\) by considering the variable \(t\) as a parameter and by applying the 'ordinary' calculation rules for differentiation.
The axial current will decrease with increasing \(x\) because some part of the flow leaks away through the membrane and leads to a membrane current \(i_m\). According to Kirchhoff's junction rule it is true that the decrease of the axial flow along the axon is equal to the membrane flow per unit length \[i_m=-\frac{\partial i_a}{\partial x}\] Substitution of the previously found formula for the axial flow gives a formula with a partial derivative of 2nd order: \[i_m=\frac{1}{r_a}\cdot\frac{\partial^2 V}{\partial x^2}\] The membrane current \(i_m\) is for the parallel connection of a resistor (with \(V=I\cdot R\)) and a capacitor (with \(Q=C\cdot V\)) equal to the sum of the two corresponding terms: \[i_m= \frac{1}{r_m}\cdot V+c_m\cdot\frac{\partial V}{\partial t}\] By setting the two expressions for the membrane current equal to each other you get: \[\begin{aligned} \frac{1}{r_a}\cdot \frac{\partial^2 V}{\partial x^2}&=\frac{1}{r_m}\cdot V+c_m\cdot\frac{\partial V}{\partial t}\\ \\ &= \frac{r_m}{r_a}\cdot \frac{\partial^2 V}{\partial x^2}=V+r_m\cdot c_m\cdot \frac{\partial V}{\partial t}\end{aligned}\] This can be rewritten as \[\lambda^2\cdot \frac{\partial^2 V}{\partial x^2}=\tau_m\cdot \frac{\partial V}{\partial t}+ V\] with \[\lambda=\sqrt{\frac{r_m}{r_a}}=\sqrt{\frac{aR_m}{2R_a}},\quad\tau_m=r_m\cdot c_m=R_m\cdot C_m\] Here, \(\lambda\) is a spacial or place constant and \(\tau_m\) is the previously introduced time constant of the cell membrane.
When the potential is \(x=0\) is kept on the value \(V_0\) and the steady state is reached (\(\frac{\partial V}{\partial t}=0\)), then we get the initial value problem \[\lambda^2\cdot \frac{\dd^2 V}{\dd x^2}=V, \qquad V(0)=V_0\] and its solution is \[V(x)=V_0\cdot e^{-\frac{x}{\lambda}}\]
Passive current flow and the cable equation
