Propagation of an action potential

Bioelectricity: Passive and activve current flow along an axon

Propagation of an action potential

In the propagation of an action potential along an axon both passive and active current flow play a role. Passive current flow has been addressed already: injected current will go along the axon, but will also leak away. When a current causes an action potential and an increase in electric potential in a neighbouring piece of the axon, the threshold value for the generation of an action potential may be reached in that region as well and generate an action potential at that spot. Due to the refractory period, the action potential will only move in one direction: from soma to the end of the axon.

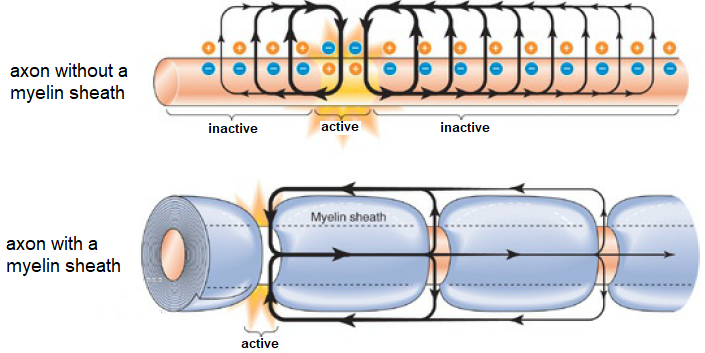
In order to increase the speed of propagation of an action potential, the axon is usually covered with myelin, which functions as an insulation layer for the leakage of current. At regular intervals there are unmyelinated spots. Here, the action potential can be regenerated. The figure below depicts the two situations described.

We will study he speed of propagation of an action potential along an axon via the model of Hodgkin and Huxley.

The position- and time-dependent model of Hodgkin and Huxley Via the cable equation we can alter the Hodgkin-Huxley model for action potentials into a model that includes a spatial dimension. When we write the cable equation as \[ \frac{1}{r_a}\cdot \frac{\partial^2 V}{\partial x^2} =\frac{1}{r_m}\cdot V+c_m\cdot\frac{\partial V}{\partial t}\] we just need to replace the term \(\frac{1}{r_m}\cdot V\), which concerns the current leakage, with the membrane current flows through the ion channels. We get: \[ \frac{1}{r_a} \frac{\partial^2 V}{\partial x^2} =c_m\frac{\partial V}{\partial t} -\overline{g_\mathrm{K}}n^4(V-E_\mathrm{K})-\overline{g_\mathrm{Na}}m^3h(V-E_\mathrm{Na})-\overline{g_\mathrm{L}}(V-E_\mathrm{L})\] Here we should consider the channel functions \(n\), \(m\) and \(h\) as position- and time-dependent, but when we can assume a constant membrane structure along the axon only time plays a role. The channel functions still satisfy the previously discussed differential equations of restricted exponential growth.

This partial differential equation cannot be exactly solved and even with numerical methods this is not easy. We will not do this, but just look at how the speed of the propagation can be described through a mathematical formula. We follow Hodgkin and Huxley, who noted that during the propagation of an action potential its shape does not change. In mathematical language this means that the action potential \(V(x,t)\) which propagates with speed \(\theta\) along the axon may be described with \(f(x-\theta t)\) for some function \(f\) in a single variable. Calculation rules for partial differentiation lead to: \[\frac{\partial^2V}{\partial x^2}=\frac{1}{\theta^2}\frac{\partial^2 V}{\partial t^2}\] The partial differential equation for the position- and time-dependent model of Hodgkin and Huxley is then an ordinary differential equation, which we can rewrite as \[ \frac{1}{r_a\theta^2}\frac{\dd^2 V}{\dd t^2} =c_m\frac{\dd V}{\dd t}-\overline{g_\mathrm{K}}n^4(V_m-E_\mathrm{K})-\overline{g_\mathrm{Na}}m^3h(V_m-E_\mathrm{Na})-\overline{g_\mathrm{L}}(V_m-E_\mathrm{L})\] This differential equation can for some choice of \(\theta\) and other parameters be solved numerically, but the problem is that we in fact want to find \(\theta\). A suitable value \(\theta\) can be found by a trial-and-improvement methods by constantly demanding that the membrane voltage is limited. We will not perform this process, but we can show how the speed depends on several electrophysiological parameters.

Speed of propagation of an action potential For the speed \(\theta\) of propagation of an action potential holds \[\theta\propto \frac{1}{C_m}\sqrt{\frac{2a}{R_aR_m}}\]

For the math enthusiast, we can make this claim plausible.

We rewrite the differential equation of order 2 as \[\left(\frac{\lambda}{\theta}\right)^2 \frac{\dd^2 V}{\dd t^2}-\tau\frac{\dd V}{\dd t}=-r_m\bigl(\overline{g_\mathrm{K}}n^4(V-E_\mathrm{K})+\overline{g_\mathrm{Na}}m^3h(V-E_\mathrm{Na})+\overline{g_\mathrm{L}}(V-E_\mathrm{L})\bigr)\] with \[\lambda=\sqrt{\frac{r_m}{r_a}}=\sqrt{\frac{a\cdot R_m}{2R_a}}\] The right-hand side concerns the ionic currents associated with an action potential. When we assume that the variation in time of the conductivity of sodium and potassium ions can be neglected, then we have al linear function of \(V\) on the right-hand side, say \(-c\cdot V+d\). So the differential equation has become a inhomogeneous, linear, 2nd order differential equation: \[\left(\frac{\lambda}{\theta}\right)^2 \frac{\dd^2 V}{\dd t^2}-\tau\frac{\dd V}{\dd t}+c\,V=d\] The general solution is the sum of a particular solution (\(V(t)=-\frac{d}{c}\) satisfies the equation), and the general solution of the corresponding homogeneous differential equation \[\left(\frac{\lambda}{\theta}\right)^2 \frac{\dd^2 V}{\dd t^2}-\tau\frac{\dd V}{\dd t}+c\,V=0\] The solution is of the form \(V(t)=V_0e^{\mu t}\) where \(\mu\) is a zero of the characteristic equation \[\left(\frac{\lambda}{\theta}\right)^2 z^2+\tau z-c=0\] Because we search for a limited function \(V\), the discriminant of the characteristic equation must be equal to 0: \[\tau - 4 \left(\frac{\lambda}{\theta}\right)^2c=0\] i.e. \[\theta=\sqrt{c}\,\frac{2\lambda}{\tau}\] The constant \(c\) depends on the properties of the ion channels in use. We can also rewrite \(\dfrac{2\lambda}{\tau}\) as \(\dfrac{1}{C_m}\sqrt{\dfrac{2a}{R_aR_m}}\).

The above formulas for the speed of propagation of an action potential along an axon indicate that the speed is proportional to the square root of the axial radius. When the specific resistances and the specific membrane capacitance are the same, then nerve fibres conduct much faster than thin fibres. In order to have a propagation that is two times faster, one needs a four times as thicker fibre.

For the giant axon of a squid we can use the following parameter values \[\begin{array}{rlrlrl} a &=\;\;0.025\,\text{cm}, & R_a &=\;\;30\,\Omega\text{cm}, & R_m &=\;\;1000\,\Omega\text{cm}^2,\\ C_m &=\;\;1\,\text{µF}/\text{cm}^2,&
\tau &=\;\;1\,\text{ms},& \lambda &=\;\;6.45\,\text{mm}\end{array}\] Then \(\dfrac{1}{C_m}\sqrt{\frac{2a}{R_aR_m}}\approx 12.9\,\text{m}/\text{s}\). The measured speed is \(21.2\,\text{m}/\text{s}\) and thus in the same order of magnitude: the needed proportionality factor would be approximately \(1.74\).

Saltatory propagation A second way to achieve a better propagation of an action potential is to decrease the time constant \(\tau= R_mC_m\) and, in particular, to decrease the membrane capacitance \(C_m\). In human physiology this is achieved by shielding the outside of a membrane with myelin; this also increases the membrane resistance, so that there may occur less current leakage along the nerve fibre via passive flow.

The shielding of an axon with myelin is on the other hand not good because the ion channels involved in the generation of an action potential cannot do their job. Therefore, the so-called myelin sheath has gaps with no myelin at regular intervals, at the so-called nodes of Ranvier. An action potential is then propagated in the myelinated part in a passive sense, and even if there is a small decrease of electric potential, then it may still be high enough to regenerate the action potential at a node of Ranvier. Thus the action potential jumps from node to node and a high speed of propagation of 100=130 m/s can be achieved. This is so-called saltatory propagation (from the Latin word "saltare" for "jumping").

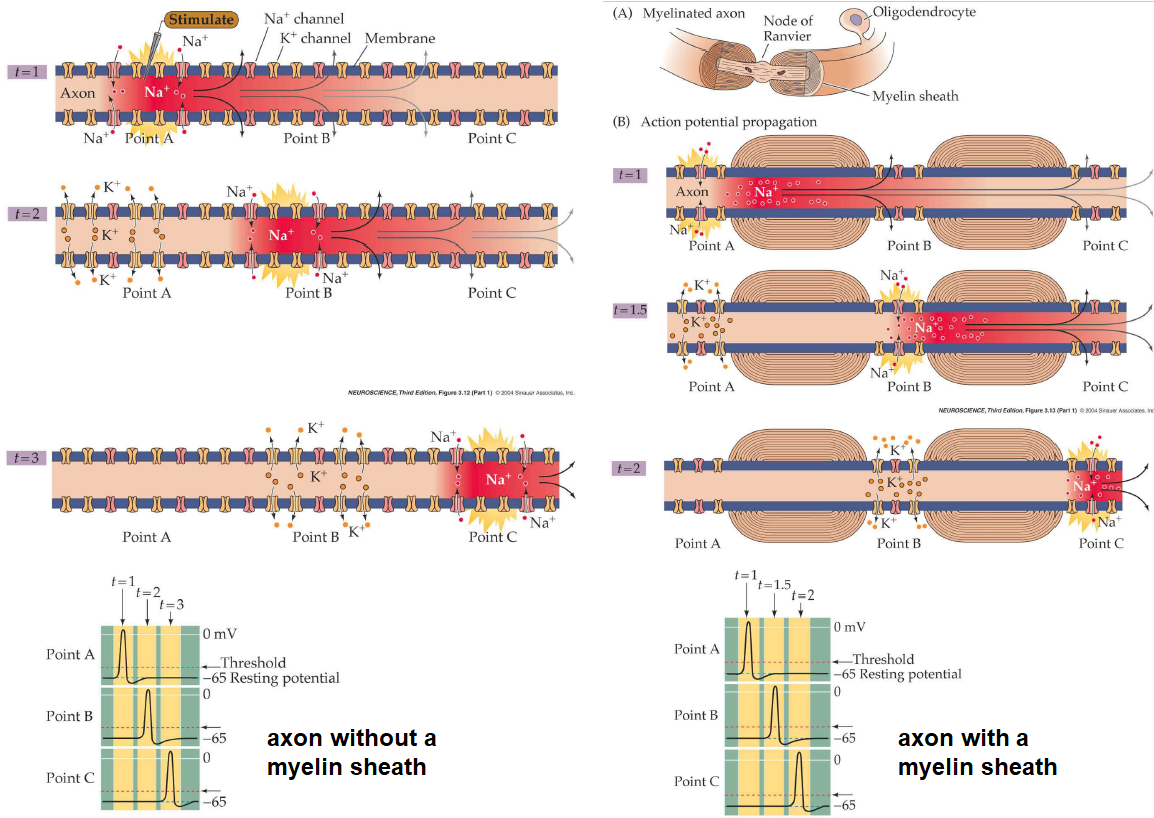
In the picture above, the processes in unmyelinated and myelinated axons are outlined. Without myelination, the propagation of an action potential along an axon will be slower and shorter. A myelin sheath with nodes of Ranvier makes regeneration of action potentials and a rapid propagation of an action potential from node to node possible.

In diseases such as multiple sclerosis, the myelin sheath is damaged and thus action potentials do not propagate well. When the myelin sheath is strongly affected, the distance between nodes of Ranvier may be to long for the propagation of an action potential and there is in fact a blockade of the nerve.