Voortgeleiding van een actiepotentiaal

Bioelektriciteit: Geleidbaarheid langs een axon

Voortgeleiding van een actiepotentiaal

Bij de voortgeleiding van een actiepotentiaal langs een axon speelt zowel passieve als actieve stroom een rol. Passieve voortgeleiding is al behandeld: geïnjecteerde stroom zal langs het axon gaan, maar ook weglekken. Wanneer een stroom een potentiaalverhoging in een naburig stukje axon te weeg brengt kan de drempelwaarde voor het genereren van een actiepotentiaal bereikt worden en in een naburig gebied ook weer een actiepotentiaal veroorzaken. Door de refractaire periode zal de actiepotentiaal zich maar in één richting kunnen bewegen: van soma naar uiteinde van het axon.

Om de snelheid van voortgeleiding van een actiepotentiaal te verhogen is het axon meestal omhult met myeline, dat als een isolatielaag voor het weglekken van stroom fungeert. Op regelmatige afstanden zijn er ongemyeliniseerde stukken. Hier kan de actiepotentiaal geregenereerd worden. Onderstaande figuur schetst de twee beschreven situaties.

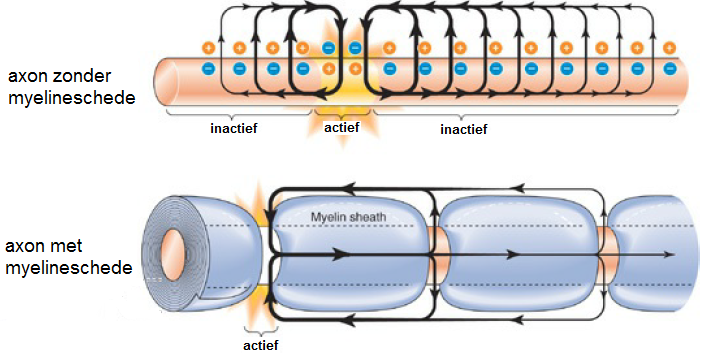
We gaan met behulp van het model van Hodgkin en Huxley de snelheid van voortgeleiding van een actiepotentiaal langs een axon bestuderen.

Plaats- en tijdafhankelijk model van Hodgkin en Huxley Met behulp van de kabelvergelijking kan het Hodgkin-Huxley model voor actiepotentialen ook tot een ruimtelijke variant omgevormd worden. Als we de kabelvergelijking opschrijven als \[ \frac{1}{r_a}\cdot \frac{\partial^2 V}{\partial x^2} =\frac{1}{r_m}\cdot V+c_m\cdot\frac{\partial V}{\partial t}\] dan hoeven we alleen maar de term \(\frac{1}{r_m}\cdot V\), die de stroomlekkage betreft, te vervangen door de membraanstroom door de ionkanalen. We krijgen dan: \[ \frac{1}{r_a} \frac{\partial^2 V}{\partial x^2} =c_m\frac{\partial V}{\partial t} -\overline{g_\mathrm{K}}n^4(V-E_\mathrm{K})-\overline{g_\mathrm{Na}}m^3h(V-E_\mathrm{Na})-\overline{g_\mathrm{L}}(V-E_\mathrm{L})\] Hierbij moeten we in principe de kanaalfunctie \(n\), \(m\) en \(h\) plaats- en tijdsafhankelijk beschouwen, maar als we een constante membraanstructuur langs het axon veronderstellen speelt alleen tijd een rol. De kanaalfuncties voldoen steeds aan de eerder besproken differentiaalvergelijkingen van begrensde exponentiële groei.

Deze partiële differentiaalvergelijking is niet exact op te lossen en zelf numeriek is dit niet gemakkelijk. We gaan dit dan ook niet doen, maar bekijken enkel hoe de snelheid van elektrische voorgeleiding in formulevorm te beschrijven is. We volgen hierbij Hodgkin en Huxley die opmerkten dat bij voortgeleiding de vorm van de actiepotentialen nagenoeg niet verandert. In wiskundige taal betekent dit dat de actiepotentiaal \(V(x,t)\) die zich met snelheid \(\theta\) voort beweegt langs het axon beschreven kan worden met \(f(x-\theta t)\) voor zekere functie in één variabele. Rekenregels voor partieel differentiëren geeft dan: \[\frac{\partial^2V}{\partial x^2}=\frac{1}{\theta^2}\frac{\partial^2 V}{\partial t^2}\] De partiële differentiaalvergelijking voor het plaats- en tijdafhankelijke model van Hodgkin en Huxley wordt dan een gewone differentiaalvergelijking die we kunnen schrijven als \[ \frac{1}{r_a\theta^2}\frac{\dd^2 V}{\dd t^2} =c_m\frac{\dd V}{\dd t}-\overline{g_\mathrm{K}}n^4(V_m-E_\mathrm{K})-\overline{g_\mathrm{Na}}m^3h(V_m-E_\mathrm{Na})-\overline{g_\mathrm{L}}(V_m-E_\mathrm{L})\] Deze differentiaalvergelijking is bij een keuze van \(\theta\) en andere parameters numeriek op te lossen, maar het probleem is dat we \(\theta\) juist te weten willen komen. Een geschikte waarde van \(\theta\) kun je met een trial-and-improve methode benaderen door steeds te eisen dat de membraanspanning begrensd blijft. We gaan dit proces niet uitvoeren. Maar we kunnen wel laten zien hoe de snelheid afhangt van enkele elektrofysiologische grootheden.

Snelheid van voortgeleiding van een actiepotentiaal Voor de snelheid \(\theta\) van voortgeleiding van een actiepotentiaal geldt \[\theta\propto \frac{1}{C_m}\sqrt{\frac{2a}{R_aR_m}}\]

Voor de liefhebber maken we de bewering aannemelijk.

We herschrijven de differentiaalvergelijking van orde 2 als \[\left(\frac{\lambda}{\theta}\right)^2 \frac{\dd^2 V}{\dd t^2}-\tau\frac{\dd V}{\dd t}=-r_m\bigl(\overline{g_\mathrm{K}}n^4(V-E_\mathrm{K})+\overline{g_\mathrm{Na}}m^3h(V-E_\mathrm{Na})+\overline{g_\mathrm{L}}(V-E_\mathrm{L})\bigr)\] met \[\lambda=\sqrt{\frac{r_m}{r_a}}=\sqrt{\frac{a\cdot R_m}{2R_a}}\] De rechterkant betreft de ionstromen die bij een actiepotentiaal horen. Als we veronderstellen dat de variatie in tijd van de geleidbaarheid van het natrium- en kaliumionen verwaarloosbaar is dan staat er aan de rechterkant een lineaire functie van \(V\), zeg \(-c\cdot V+d\). Hiermee is de differentiaalvergelijking een lineaire inhomogene 2de orde differentiaalvergelijking geworden: \[\left(\frac{\lambda}{\theta}\right)^2 \frac{\dd^2 V}{\dd t^2}-\tau\frac{\dd V}{\dd t}+c\,V=d\] De algemene oplossing is de som van een specifieke oplossing (\(V(t)=-\frac{d}{c}\) voldoet) en de algemene oplossing van de bijpassende homogene \[\left(\frac{\lambda}{\theta}\right)^2 \frac{\dd^2 V}{\dd t^2}-\tau\frac{\dd V}{\dd t}+c\,V=0\] De oplossing is van de vorm \(V(t)=V_0e^{\mu t}\) met \(\mu\) nulpunt van de karakteristieke vergelijking \[\left(\frac{\lambda}{\theta}\right)^2 z^2+\tau z-c=0\] Omdat we een begrensde functie \(V\) zoeken zal de discriminant van de karakteristieke vergelijking gelijk aan 0 moeten zijn: \[\tau - 4 \left(\frac{\lambda}{\theta}\right)^2c=0\] oftewel \[\theta=\sqrt{c}\,\frac{2\lambda}{\tau}\] De constante \(c\) hangt van de eigenschappen van de gebruikte ionkanalen af. We kunnen \(\dfrac{2\lambda}{\tau}\) ook schrijven als \(\dfrac{1}{C_m}\sqrt{\dfrac{2a}{R_aR_m}}\).

Aan bovenstaande formules voor de snelheid van voortgeleiding van een actiepotentiaal langs een axon kun je zien dat de snelheid evenredig is met de wortel van de axiale straal. Wanneer de specifieke weerstanden en de de specifieke membraancapaciteit gelijk zijn geleiden dikkere zenuwvezels dus sneller dan dunne vezels. Om een 2 keer zo snelle voortgeleiding te krijgen zou de zenuw 4 keer zo dik moeten zijn.

Voor de reuze-zenuwvezel van een pijlinktvis kunnen we de volgende parameterwaarden gebruiken \[\begin{array}{rlrlrl} a &=\;\;0.025\,\text{cm}, & R_a &=\;\;30\,\Omega\text{cm}, & R_m &=\;\;1000\,\Omega\text{cm}^2,\\ C_m &=\;\;1\,\text{µF}/\text{cm}^2,&
\tau &=\;\;1\,\text{ms},& \lambda &=\;\;6.45\,\text{mm}\end{array}\] Dan is \(\dfrac{1}{C_m}\sqrt{\frac{2a}{R_aR_m}}\approx 12.9\,\text{m}/\text{s}\). De gemeten snelheid is \(21.2\,\text{m}/\text{s}\) en dus in dezelfde orde van grootte: de benodigde evenredigheidfactor zou dus ongeveer \(1.74\) zijn.

Saltatoire voortgeleiding Een tweede manier om een betere voortgeleiding van een actiepotentiaal te bewerkstelligen is een verkleining van de tijdconstante \(\tau= R_mC_m\) en in het bijzonder door de verlaging van de membraancapaciteit \(C_m\). In humane fysiologie gebeurt dat door de buitenkant van een membraan met myeline af te schermen; tevens verhoogt dit de membraanweerstand zodat er minder stroomlekkage kan optreden langs de zenuwvezel via passieve stroming.

De omhulling van een axon met myeline is ook weer niet goed omdat dan de ionkanalen die betrokken zijn bij vorming van actiepotentialen hun werk dan niet meer kunnen doen. Daarom wordt de zogenaamde myelineschede op regelmatige afstand ingesnoerd of zelf onderbroken door een kort ongemyeliniseerd stukje zenuwvezel, de zogenaamde insnoeringen of knopen van Ranvier. Een actiepotentaal wordt dan in het gemyeliniseerde deel voortgeleid in passieve zin, en ook als er een kleine potentiaalvermindering heeft plaats gevonden, dan kan deze nog hoog genoeg zijn om in de knoop van Ranvier de actiepotentiaal te laten regenereren. Zo springt de actiepotentiaal van knoop naar knoop en kan een hoge snelheid van voortgeleiding met 100-130 m/s gehaald worden. Dit heet saltatoire voortgeleiding (van het latijnse woord "saltare" voor "springen").

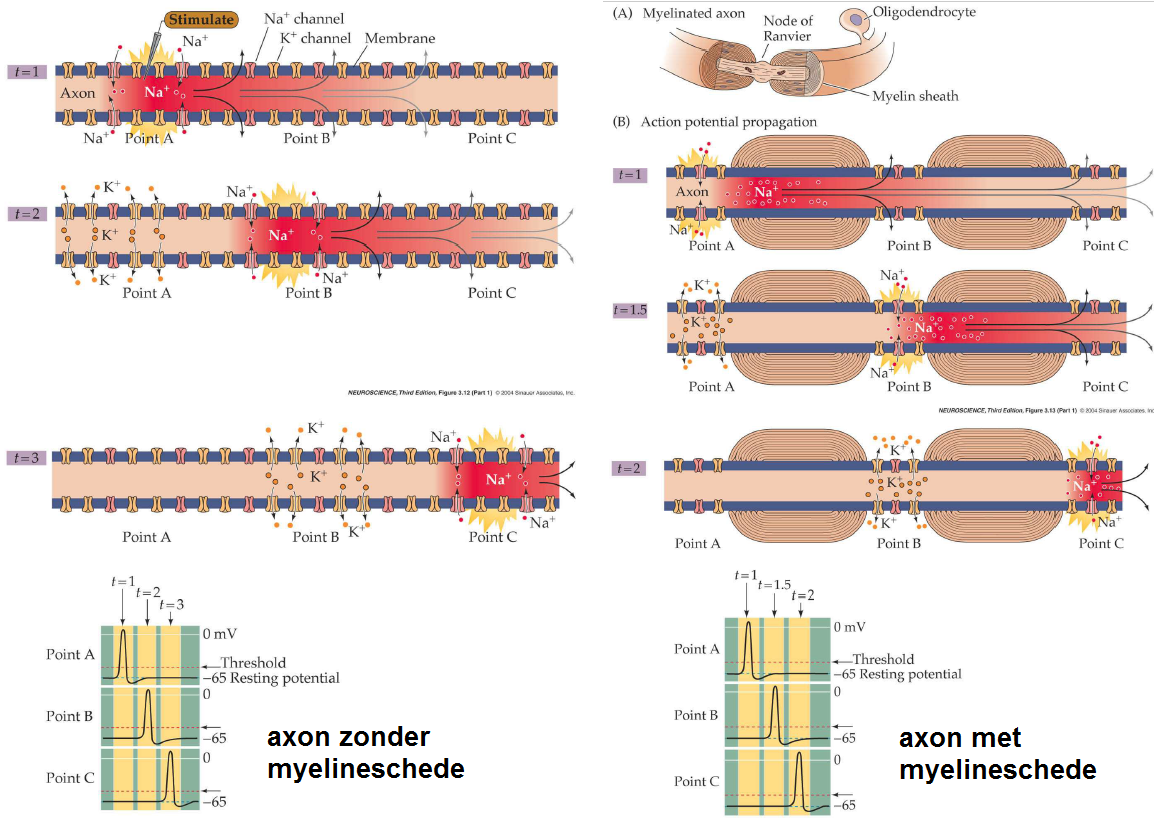
In bovenstaand plaatje zijn de processen in een ongemyeliniseerd axon en gemyeliniseerd axon geschetst. Zonder myelinatie zal een actiepotentieel minder snel en minder lang zich kunnen voortbewegen langs een axon. Een myelineschede met knopen van Ranvier maakt regeneratie van actiepotentialen en het snel voortbewegen van een actiepotentiaal van knoop naar knoop mogelijk.

Bij ziektes zoals Multiple Sclerose wordt de myelineschede aangetast en daardoor worden actiepotentialen minder goed voortgeleid. Als de myelineschede sterk is aangetast kan zelfs de afstand tussen knopen van Ranvier niet meer gehaald wordt in de voortgeleiding van een actiepotentiaal en is er dus sprake van een blokkade van de zenuw.