The tangent function has on the interval \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) an inverse function called arctangent and denoted \(\arctan\); so \[\tan\bigl(\arctan(x)\bigr)=x\tiny.\] The graph of \(\arctan\) looks like this:

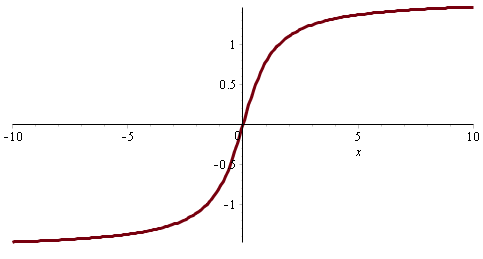
It follows from the definition that \(\arctan(1)=\frac{\pi}{4}\) and therefore \[\pi=4\arctan(1)\tiny.\] If we can calculate a good approximation of \(\arctan(1)\), then we can find a good approximation of the number \(\pi\). We do this by first determining a Taylor series approximation of the arctangent function.

For the derivative of the tangent function holds: \[\frac{\dd \tan(x)}{\dd x}=\frac{1}{\cos^2x}=1+\tan^2(x)\tiny.\] From the chain rule it follows with \(u=\arctan(x)\) that \[\frac{\dd \tan(u)}{\dd u}\cdot \frac{\dd u}{\dd x}=1\] and therefore \[\bigl(1+\tan^2(u)\bigr)\cdot\frac{\dd \arctan(x)}{\dd x}=1\] or \[(1+x^2)\cdot\frac{\dd \arctan(x)}{\dd x}=1\] In other words: \[\frac{\dd \arctan(x)}{\dd x}=\frac{1}{1+x^2}\tiny.\] The Taylor series of the right-hand side about \(x=0\) can easily be calculated: \[\frac{1}{1+x^2}=1-x^2+x^4-x^6+x^8-x^{10}+\cdots=\sum_{k=0}^{\infty}(-1)^k\cdot x^{2k}\tiny.\] But then we can also find a series whose derivative is equal to the above Taylor series; this is per construction the Taylor series of \(\arctan(x)\) about \(x=0\). We get: \[\arctan(x) = x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\frac{1}{9}x^9-\frac{1}{11}x^{11}+\cdots=\sum_{k=0}^{\infty}\frac{(-1)^{k}}{2k+1}\cdot x^{2k+1}\tiny.\]