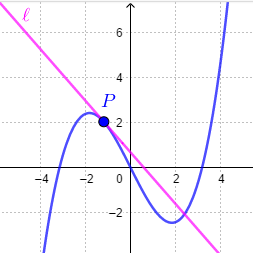
Differentiation, derivatives and Taylor approximations: Tangent line
 Derivative of a function
Derivative of a function
Below, the graph of a smooth function \(f(t)\) has been plotted together with the tangent line at the point \((a,f(a))\). In the immediate neighbourhood of this point, the graph and the tangent line can hardly be distinguished. As an illustration of this, the marked rectangle around the point \((a,f(a))\) in the figure below is displayed in an enlarged format.
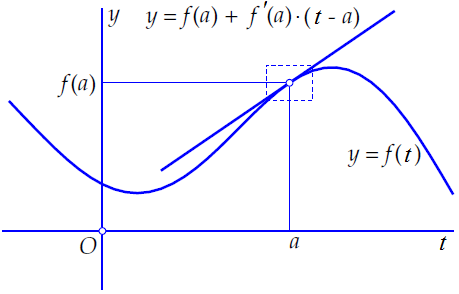
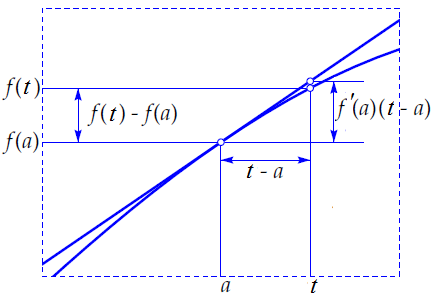
In the below interactive diagram you can explore this behaviour. Yan can drag the point \(A\) over the graph and zoom in on the situation around this point by making the marked square around the point smaller: the drawn tangent line and the graph of the function are then more similar.
For a smooth function \(f\) it is true that when \(t\) gets close to a fixed\(a\) the following approximation is valid: \[\frac{f(t)-f(a)}{t-a}\approx \frac{m\cdot (t-a)}{t-a}=m\] where \(m\) is a constant equal to the slope of the graph of \(f\). More precisely: \[m=\lim_{t\to a} \frac{f(t)-f(a)}{t-a}\] One calls \(m\) the derivative of \(f(t)\) in \(a\) and denotes this as \(f'(a)\) and as \(\displaystyle\frac{df}{dt}(a)\) or \(\displaystyle\frac{\dd f}{\dd t}\bigg\vert_{t=a}\).
The equation of the tangent line \(\ell\) at the point \((a,f(a))\) is equal to \[y=f(a)+f'(a)\cdot(t-a).\] For \(t\) close to \(a\) we have: \[f(t)\approx f(a)+ f'(a)\cdot(t-a)\tiny.\]
In the interactive diagram to the right you can drag the point \(P\) over the graph and observe the tangent line at that point.
The above statement also means that when the function value and derivatives for a certain \(t\) are known, one also can estimate the function values at a distance \({\vartriangle}t\) with the following formula: \[f(t+{\vartriangle}t )\approx f(t)+ f'(t)\cdot {\vartriangle}t \tiny.\] The closer to \(t\) (or the smaller the stepsize \({\vartriangle}t\)), the better the estimated value of the function.
For a smooth function \(f(t)\) over an interval there is at any point \(t\) a derivative \(f'(t)\) over that interval defined: \[f'(t)=\lim_{{\vartriangle}t\to 0}\frac{f(t+{\vartriangle}t)-f(t)}{{\vartriangle}t}\] Thus the derivative over the interval itself is a function, also called the derivative. Common notations for the derivative of \(f(t)\) are \(f'\), \(\displaystyle\frac{\dd f}{\dd t}\), \(f'(t)\), \(\displaystyle\frac{\dd f}{\dd t}(t)\) and \(\displaystyle\frac{\dd}{\dd t}f(t)\). The process of computing a derivative of a given function is called differentiation.
Let us calculate the derivative of the polynomial function of degree 2 from a previous example.
For the polynomial function \(f(t)=3t^2-2t-1\) we calculate the difference quotient over the interval \([t,t+{\vartriangle}t]\) .
\[\begin{aligned}
\frac{{\vartriangle}f}{{\vartriangle}t} &= \frac{f(t+{\vartriangle}t)-f(t)}{{\vartriangle}t} \\ \\
&= \frac{\left(3(t+{\vartriangle}t)^2-2(t+{\vartriangle}t)-1\right) - \left(3t^2-2t-1\right)}{{\vartriangle}t} \\ \\
&= \frac{\left(3t^2+6t{\vartriangle}t+3({\vartriangle}t)^2 - 2(t+{\vartriangle}t)-1\right) - \left(3t^2-2t-1\right)}{{\vartriangle}t} \\ \\
&= \frac{6t{\vartriangle}t+3({\vartriangle}t)^2 - 2{\vartriangle}t}{{\vartriangle}t} \\ \\
&= 6t-2+3{\vartriangle}t\\ \\
&\to 6t-2\quad\mathrm{als\;}{\vartriangle}t \to 0
\end{aligned}\] So: \(f'(t)=6t-2\).
Computing a derivative in the above manner is cumbersome, but fortunately derivatives of many standard functions is listed and there exist calculation rules to differentiate combinations of functions efficiently. An example of such rule is the constant factor rule voor differentiation a multiple of a function for which the derivative is known.
Constant factor rule If \(f\) is a function of which the derivative \(f'\) is known, then we have: \[\bigl(c\cdot f(t)\bigr)' = c\cdot f'(t)\quad \text{for every constant }c\]
Mathcentre video
Differentiation First Principles - Tangent (30:44)