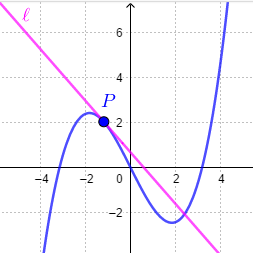
Differentiëren, afgeleide functies en Taylorbenaderingen: Raaklijn
 Afgeleide functie
Afgeleide functie
Hieronder is de grafiek van een nette functie \(f(t)\) getekend, met daarbij ook de raaklijn in het punt \((a,f(a))\). Vlak in de buurt van dit punt zijn de grafiek en de raaklijn nauwelijks van elkaar te onderscheiden. Als illustratie hiervan is het rechthoekje rond het punt \((a,f(a))\) in de figuur eronder nog eens vergroot weergegeven.
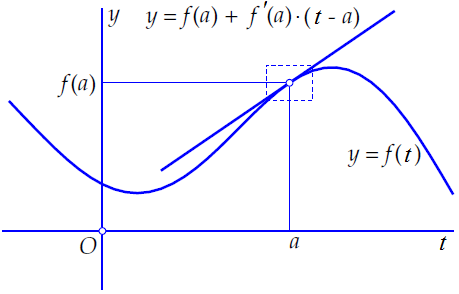
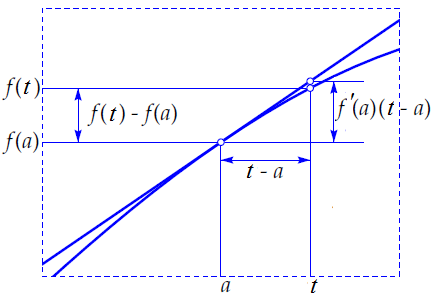
In onderstaand interactief diagram kun je dit gedrag ook onderzoeken. Je kunt het punt \(A\) over de grafiek slepen en door het vierkant te verkleinen inzoomen op het punt: de getekende raaklijn en de grafiek van de functie lijken dan meer op elkaar.
Voor een 'nette' functie \(f\) geldt voor \(t\) vlak bij een vast gekozen \(a\) dat \[\frac{f(t)-f(a)}{t-a}\approx \frac{m\cdot (t-a)}{t-a}=m\] waarbij \(m\) een constante gelijk aan de helling van de grafiek van \(f\) is. Preciezer geformuleerd: \[m=\lim_{t\to a} \frac{f(t)-f(a)}{t-a}\] Men noemt \(m\) de afgeleide van \(f\) in \(a\) en noteert dit met \(f'(a)\) en met \(\displaystyle\frac{\dd f}{\dd t}(a)\) of \(\displaystyle\frac{\dd f}{\dd t}\bigg\vert_{t=a}\).
De vergelijking van de raaklijn \(\ell\) in het punt \((a,f(a))\) is gelijk aan \[y=f(a)+f'(a)\cdot(t-a).\] Voor \(t\) in de buurt van \(a\) geldt dus: \[f(t)\approx f(a)+ f'(a)\cdot(t-a)\tiny.\]
In nevenstaande interactieve figuur kun je het punt \(P\) verslepen over de grafiek en de raaklijn in dat punt bekijken.
Bovenstaande betekent ook dat als de functiewaarde en afgeleiden voor een zekere \(t\) bekend zijn, men ook functiewaarden op afstand \({\vartriangle}t\) goed kan schatten met de volgende formule: \[f(t+{\vartriangle}dt)\approx f(t)+ f'(t)\cdot {\vartriangle}t\tiny.\] Hoe dichter in de buurt van \(t\) (ofwel hoe kleiner de stapgrootte \({\vartriangle}t\)), des te beter is de schatting van de functiewaarde. In het limietgeval stappen we van een differentiequotiënt \(\dfrac{{\vartriangle}f}{{\vartriangle}t}\) over op een differentiaalquotiënt \(\dfrac{{\dd}f}{{\dd}t}\), meestal afgeleide \(f'(t)\) in het punt \(t\) genoemd.
Voor een 'nette' functie \(f(t)\) op een interval is er in elk punt \(t\) van dat interval een afgeleide \(f'(t)\) gedefinieerd: \[f'(t)=\lim_{{\vartriangle}t\to 0}\frac{f(t+{\vartriangle}t)-f(t)}{{\vartriangle}t}\] Daarmee is de afgeleide op het interval zelf een functie geworden, de afgeleide functie. Veelgebruikte notaties voor de afgeleide functie van \(f(t)\) zijn \(f'\), \(\displaystyle\frac{\dd f}{\dd t}\), \(f'(t)\), \(\displaystyle\frac{\dd f}{\dd t}(t)\) en \(\displaystyle\frac{\dd}{\dd t}f(t)\). Het bepalen van een afgeleide van een gegeven functie heet differentiëren.
Laten we de afgeleide functie voor de tweedegraads veeltermfunctie uit een eerder voorbeeld eens uitrekenen.
Voor de kwadratische functie \(f(t)=3t^2-2t-1\) berekenen we het differentiequotiënt over het tijdsinterval \([t,t+{\vartriangle}t]\).
\[\begin{aligned}
\frac{{\vartriangle}f}{{\vartriangle}t} &= \frac{f(t+{\vartriangle}t)-f(t)}{{\vartriangle}t} \\ \\
&= \frac{\left(3(t+{\vartriangle}t)^2-2(t+{\vartriangle}t)-1\right) - \left(3t^2-2t-1\right)}{{\vartriangle}t} \\ \\
&= \frac{\left(3t^2+6t{\vartriangle}t+3({\vartriangle}t)^2 - 2(t+{\vartriangle}t)-1\right) - \left(3t^2-2t-1\right)}{{\vartriangle}t} \\ \\
&= \frac{6t{\vartriangle}t+3({\vartriangle}t)^2 - 2{\vartriangle}t}{{\vartriangle}t} \\ \\
&= 6t-2+3{\vartriangle}t\\ \\
&\approx 6t-2\quad\text{als}\quad{\vartriangle}t \approx 0
\end{aligned}\] Dus: \(f'(t)=6t-2\).
Het bepalen van een afgeleide op bovenstaande wijze is omslachtig, maar gelukkig bestaan er lijstjes met afgeleiden van standaardfuncties en rekenregels om efficiënt functies te differentiëren bij combinaties van functies. Een voorbeeld van zo'n rekenregel is de constante factorregel voor het differentiëren van een functie die een veelvoud is van een andere functie.
Constante factorregel Als \(f\) een functie is waarvan de afgeleide \(f'\) bekend is, dan geldt: \[\bigl(c\cdot f(t)\bigr)' = c\cdot f'(t)\quad \text{voor elke constante }c\]
Mathcentre video
Differentiation First Principles - Tangent (30:44)