Derivatives of exponential functions

Differentiation, derivatives and Taylor approximations: Differentiating exponential and logarithmic functions

Derivatives of exponential functions

Recall that the exponential function \(f(x)=e^x\) has been introduced as the exponential function with such a base (indicated by \(e\) ) that the graph of \(f\) and the straight line with equation \(y=x+1\) touch each other at the point \((0,1)\).

grafiek van de exponentiële functie

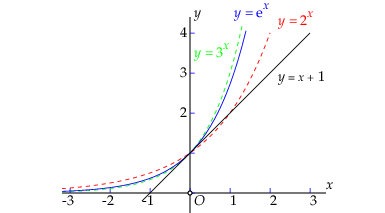
This means that the function values of \(f(x)\) and \(y(x)=1+x\) differ little from one another for small values of \(x\). In other words, \(e^{{\vartriangle}x}\approx 1+{\vartriangle}x\) for small \({\vartriangle}x\), or \[\frac{e^{{\vartriangle}x}-1}{{\vartriangle}x}\to 1\text{ when}{\vartriangle}x\to 0\] For the difference quotient of \(f\) therefore holds \[\begin{aligned} \frac{{\vartriangle}f}{{\vartriangle}x} &= \frac{e^{x+{\vartriangle}x}-e^x}{{\vartriangle}x} \\ \\
&= \frac{e^x\cdot e^{{\vartriangle}x}-e^x}{{\vartriangle}x}\\ \\
&= \frac{e^x\cdot \left(e^{{\vartriangle}x}-1\right)}{{\vartriangle}x}\\ \\
&= e^x\cdot \frac{ e^{{\vartriangle}x}-1}{{\vartriangle}x}\\ \\
&\to e^x\text{ when }{\vartriangle}x\to 0\end{aligned}\]

We have just demonstrated that the derivative of the exponential function \(f(x)=e^x\) is equal to the function itself. This is the important thing to remember.

Derivative of the exponential function If \(f(x)=e^x\) then \(f'(x)=e^x\)

The derivative of the exponential function \(f(x)=e^x\) is equal to the function itself. So, this function has the property that \(f'(x)=f(x)\). This is not the only function with this property: the function \(g(x)=c\cdot e^x\), with constant \(c\), has the same equality.

The derivative of an exponential function with any base can be found with the above result and previous calculation rules. But actually, you have to know the derivative of this standard function by heart.

Derivative of an exponential function with base a If \(f(x)=a^x\) then \(f'(x)=a^x\cdot \ln(a)\) for any base \(a>0\).

For math enthusiasts we provide the mathematical proof of \(\left(a^x\right)'=a^x\cdot \ln(a)\).

First we write the function in a different way: \(f(x)=a^x=e^{\ln(a^x)}=e^{x\ln(a)}=(e^x)^{\ln(a)}\) .
With the chain rule and the derivative of a power function, we can now differentiate \(f(x)\): \[\begin{aligned}f'(x)&=\left((e^x)^{\ln(a)}\right)'\\
&=\ln(a)\cdot (e^x)^{\ln(a)-1}\cdot\left(e^x\right)'\\
&=\ln(a)\cdot (e^x)^{\ln(a)-1}\cdot e^x\\
&=\ln(a)\cdot (e^x)^{\ln(a)}\\
&=\ln(a)\cdot a^x\end{aligned}\]

Calculate the derivative of \(f(r)=2\cdot 7^r\)

\[\begin{aligned}f'(r)&=2\cdot\Bigl( 7^{r}\Bigr)'\\ &=2\cdot 7^{r} \cdot \ln(7)\\ &=2 \cdot \ln(7)\cdot 7^{r}\end{aligned}\] Note that the function \(f(r)\) has the following property: \(f'(r)=\ln(7)\cdot f(r)\) .

New example

Finally we present an interactive diagram to illustrate that exponential functions have derivatives that are multiples of exponential functions and that the base \(e\) matches the special exponential function that is its own derivative. Drag the slider to select bases between \(2\) and \(5\) and watch in the diagram on the right-hand side how the derivatives of \(f_a(x)=a^x\) relate to the special exponential function \(f_e(x)=e^x\) (the blue graph) for various values of \(a\).

GeoGebra