Afgeleiden van exponentiële functies

Differentiëren, afgeleide functies en Taylorbenaderingen: Differentiëren van exponentiële en logaritmische functies

Afgeleiden van exponentiële functies

We roepen in herinnering dat dé exponentiële functie \(f(x)=e^x\) geïntroduceerd is als de exponentiële functie met een zodanig grondtal (aangeduid met \(e\)) dat de grafiek van \(f\) en de rechte lijn met vergelijking \(y=x+1\) elkaar raken in het punt \((0,1)\).

grafiek van de exponentiële functie

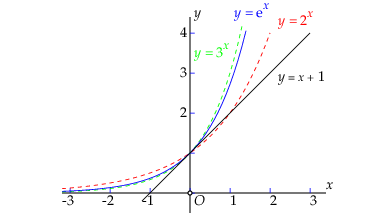
Dit betekent dat de functiewaarden van \(f(x)\) en \(y(x)=1+x\) weinig van elkaar verschillen voor kleine waarden van \(x\). Met andere woorden: \(e^{{\vartriangle}x}\approx 1+{\vartriangle}x\) voor kleine \({\vartriangle}x\), oftewel \[\frac{e^{{\vartriangle}x}-1}{{\vartriangle}x}\to 1\text{ als }{\vartriangle}x\to 0\] Voor het differentiequotiënt van \(f\) geldt dus \[\begin{aligned} \frac{{\vartriangle}f}{{\vartriangle}x} &= \frac{e^{x+{\vartriangle}x}-e^x}{{\vartriangle}x} \\[0.25cm]
&= \frac{e^x\cdot e^{{\vartriangle}x}-e^x}{{\vartriangle}x}\\[0.25cm]
&= \frac{e^x\cdot \left(e^{{\vartriangle}x}-1\right)}{{\vartriangle}x}\\[0.25cm]
&= e^x\cdot \frac{ e^{{\vartriangle}x}-1}{{\vartriangle}x}\\[0.25cm]
&\to e^x\text{ als }{\vartriangle}x\to 0\end{aligned}\]

We hebben zojuist bewezen dat de afgeleide van dé exponentiële functie \(f(x)=e^x\) gelijk is aan de functie zelf. Dit is het belangrijkste om te onthouden.

Afgeleide van de exponentiële functie Als \(f(x)=e^x\) dan \(f'(x)=e^x\)

De afgeleide van de exponentiële functie \(f(x)=e^x\) is gelijk aan de functie zelf. Deze functie heeft dus de eigenschap dat \(f'(x)=f(x)\). Dit is niet de enige functie met deze eigenschap: voor de functie \(g(x)=c\cdot e^x\), met constante \(c\), geldt dit ook.

Met bovenstaand resultaat en eerdere rekenregels kan de afgeleide voor een exponentiële functie met elk grondtal gevonden worden. Maar eigenlijk moet je de afgeleide van deze standaardfunctie uit het hoofd leren.

Afgeleide van een exponentiële functie met grondtal a Als \(f(x)=a^x\) dan \(f'(x)=a^x\cdot \ln(a)\) voor elk grondtal \(a>0\).

Voor de liefhebber geven we het wiskundige bewijs van \(\left(a^x\right)'=a^x\cdot \ln(a)\).

Eerst schrijven we de functie anders op: \(f(x)=a^x=e^{\ln(a^x)}=e^{x\ln(a)}=(e^x)^{\ln(a)}\).
Met de kettingregel en de afgeleide voor een machtsfunctie kunnen we nu \(f(x)\) differentiëren: \[\begin{aligned}f'(x)&=\left((e^x)^{\ln(a)}\right)'\\
&=\ln(a)\cdot (e^x)^{\ln(a)-1}\cdot\left(e^x\right)'\\
&=\ln(a)\cdot (e^x)^{\ln(a)-1}\cdot e^x\\
&=\ln(a)\cdot (e^x)^{\ln(a)}\\
&=\ln(a)\cdot a^x\end{aligned}\]

Bereken de afgeleide van \(f(t)=6\cdot 19^t\)

\[\begin{aligned}f'(t)&=6\cdot\Bigl( 19^{t}\Bigr)'\\[0.25cm] &=6\cdot 19^{t} \cdot \ln(19)\\[0.25cm]&=6 \cdot \ln(19)\cdot 19^{t}\end{aligned}\] Merk op dat de functie \(f(t)\) de volgende eigenschap bezit: \(f'(t)=\ln(19)\cdot f(t)\).

Nieuw voorbeeld

Tot slot geven we een interactief diagram om te illustreren dat exponentiële functies afgeleiden bezitten die zelf ook weer veelvouden van exponentiële functies zijn en dat het grondtal \(e\) past bij dié exponentiële functie die zichzelf als afgeleide heeft. Beweeg maar een de schuifbalk om grondtallen tussen \(2\) en \(5\) te kiezen en zie in de rechterkant van het diagram hoe de afgeleide functies van \(f_a(x)=a^x\) zich verhouden tot dé exponentiéle functie \(f_e(x)=e^x\) (de blauwe grafiek) voor verschillende waarden van \(a\).

GeoGebra