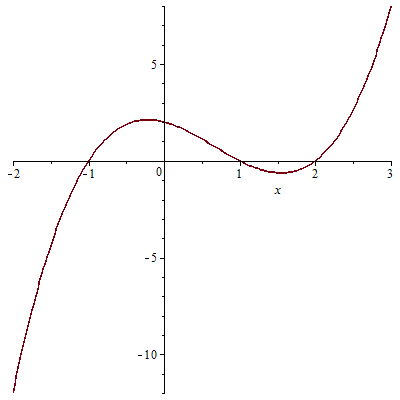
We determine all stationary points and inflection points of the polynomial function

$$f(x)=x^3-2x^2-x+2$$ The graph of $f(x)$ on the interval $(-2,3)$ is as follows:

We calculate the first, second and third derivative of $f(x)$:

$$\begin{aligned} f'(x) &= 3x^2-4x-1\\ f''(x) &=6x-4 \\ f'''(x)&=6\end {aligned}$$

In order to find all critical points of $f(x)$ we start with solving the equation $f'(x)=0$. Because the first derivative is a quadratic function, we can use the abc-formula:

$$3x^2-4x-1=0\iff x=\frac{-(-4)\pm\sqrt{(-4)^2-4\times 3\times -1}}{2\times 3}=\frac{2}{3}\pm\frac{1}{3}\sqrt{7}$$ The critical values are thus approximately equal to $x_1\approx -0.22$ and $x_2\approx 1.55$. From the graph we read off that the first point is a local maximum and a second local minimum.

Via the second derivative test we can determine the nature of the calculated critical points.

$$\begin{aligned} f''\bigl(\tfrac{2}{3}-\tfrac{1}{3}\sqrt{7}\bigr)=-2\sqrt{7}<0&\implies x=\tfrac{2}{3}-\tfrac{1}{3}\sqrt{7}\;\text{ is a local maximum}\\ f''\bigl(\tfrac{2}{3}+\tfrac{1}{3}\sqrt{7}\bigr)=2\sqrt{7}>0&\implies x=\tfrac{2}{3}+\tfrac{1}{3}\sqrt{7}\;\text{ is a local minimum}\end{aligned}$$ These are indeed local extrema because the function $f(x)$ resembles the cubic function $x^3$ for large $x$ and this function has no global maximum or minimum.

In order to find all all inflection points of $f(x)$ we must solve the equation $f''(x)=0$. In this case it is the linear equation $6x-4=0$ and the solution is $\displaystyle x=\tfrac{2}{3}$. Because $f'''(x)=6\neq 0$, the calculated point is indeed an inflection point of the function $f(x)$. The derivative is in this point not equal to zero, but $\displaystyle f'(\tfrac{2}{3})=-\tfrac{7}{3}$. The tangent line at the inflection point is thus a downward straight line (with equation $\displaystyle y=-\tfrac{7}{3}x+\tfrac{63}{27}$) that cuts the graph of $f(x)$, as can be seen in the following diagram.