We bepalen alle stationaire punten en buigpunten van de veeltermfunctie \[f(x)=x^3-2x^2-x+2\] De grafiek van \(f(x)\) op het interval \((-2,3)\) is als volgt:

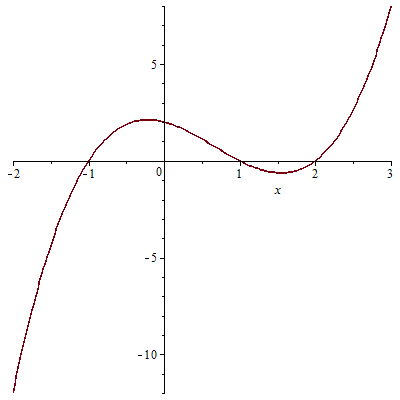
We berekenen de eerste, tweede en derde afgeleide van \(f(x)\): \[\begin{aligned} f'(x) &= 3x^2-4x-1\\ f''(x) &=6x-4 \\ f'''(x)&=6\end{aligned}\]

Om alle stationaire punten van \(f(x)\) te vinden beginnen we met het oplossen van de vergelijking \(f'(x)=0\). Omdat de eerste afgeleide een kwadratische functie is kunnen we de abc-formule gebruiken: \[3x^2-4x-1=0\iff x=\frac{-(-4)\pm\sqrt{(-4)^2-4\times 3\times -1}}{2\times 3}=\frac{2}{3}\pm\frac{1}{3}\sqrt{7}\] Bij benadering zijn de stationaire punten dus \(x_1\approx -0.22\) en \(x_2\approx 1.55\). Uit de grafiek lezen we af dat het eerste punt een lokaal maximum is en het tweede een lokaal minimum.

Met het criterium van de tweede afgeleide kunnen we de aard van de berekende stationaire punten vaststellen. \[\begin{aligned} f''\bigl(\tfrac{2}{3}-\tfrac{1}{3}\sqrt{7}\bigr)=-2\sqrt{7}<0&\implies x=\tfrac{2}{3}-\tfrac{1}{3}\sqrt{7}\;\text{ is een lokaal maximum}\\ f''\bigl(\tfrac{2}{3}+\tfrac{1}{3}\sqrt{7}\bigr)=2\sqrt{7}>0&\implies x=\tfrac{2}{3}+\tfrac{1}{3}\sqrt{7}\;\text{ is een lokaal minimum}\end{aligned}\] Het betreft inderdaad lokale extrema omdat de functie \(f(x)\) voor grote \(x\) sterk lijkt op de kubische functie \(x^3\) en deze functie geen globaal maximum of minimum heeft.

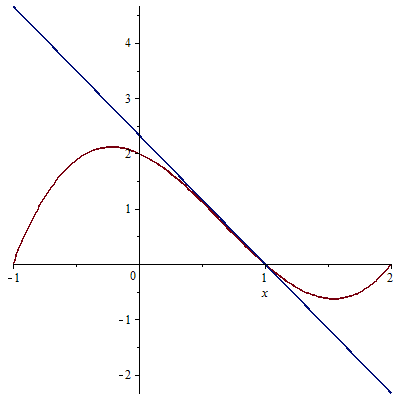
Om alle buigpunten van \(f(x)\) te vinden moeten we de vergelijking \(f''(x)=0\) oplossen. In dit geval gaat het om de lineaire vergelijking \(6x-4=0\) en de oplossing hiervan is gelijk aan \(\displaystyle x=\tfrac{2}{3}\). Omdat \(f'''(x)=6\neq 0\) is het berekende punt inderdaad een buigpunt van de functie \(f(x)\). De afgeleide is in dit punt niet gelijk aan nul, maar \(\displaystyle f'(\tfrac{2}{3})=-\tfrac{7}{3}\). De raaklijn in het buigpunt is dus een neergaande rechte lijn (met vergelijking \(\displaystyle y=-\tfrac{7}{3}x+\tfrac{63}{27}\)) die de grafiek van \(f(x)\) snijdt, zoals in onderstaand diagram te zien is.