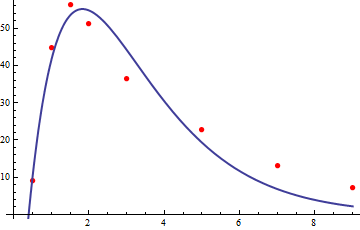
Suppose that after intake of the beta-blocker propranolol, which is for example used for lowering the blood pressure, the concentration of the drug in the blood plasma (µg/L) at time \(t\) (h) (after intake) is given by the function \[C(t)=105\,(t-0.4)\, e^{-0.75(t-0.4)}\] The question is at what time the concentration is at a maximum and which maximum value is attained.

We calculate the derivative using the differentiation rules. \[\begin{aligned} C'(t) &= 105\cdot e^{-0.75(t-0.4)} + 105\cdot (t-0.4)\cdot (-0.75)\cdot e^{-0.75(t-0.4)} \\ \\ &= 105\cdot e^{-0.75(t-0.4)}\cdot\bigl(1-0.75(t-0.4)\bigr) \\ \\ &= 105\, e^{-0.75(t-0.4)}\,(1.3-0.75t)\end{aligned}\] To find an extremum we solve the equation \(C'(t)=0\): because the exponential function is positive, the following equality must be valid \(1.3-0.75t =0\), that is, \(t\approx 1.7\). The plasma concentration is maximal after roughly one and three quarters of an hour.

This is not an artificial example because the diagram below displays the graph of this function along with measurements of the plasma concentration which come from a study of plasma levels after simultaneous oral and intravenous administration of propranolol [Source: Olanoff, L. , et. al., (1986). Clinical Pharmacology and Therapeutics, 40, 408-414]. The number \(0.4\) that in combination with time \(t\) repeatedly occurs in this formula is the estimated delay time of the drug upon oral administration, that is, the time required before the drug passes from the stomach into the small intestine and then is absorbed via the portal vein. If we translate the time scale to this point in time and fix here the origin \(t=0\), then the formula for the plasma concentration would simplify to \(C(t)=105\,t\, e^{-0.75t}\), but this does not make much difference for the calculation of the maximum.