Stel dat na het innemen van de bètablokker propranolol, die onder meer gebruikt wordt voor het verlagen van de bloeddruk, de concentratie van het farmacon in het bloedplasma (#\mathrm{µ}#g/L) op tijdstip \(t\) (uur) na inname gegeven is door de functie \[C(t)=105\,(t-0.4)\, e^{-0.75(t-0.4)}\] De vraag is op welk tijdstip de concentratie het grootst is en welke maximale waarde aangenomen wordt.

We bereken de afgeleide met behulp van de rekenregels. \[\begin{aligned} C'(t) &= 105\cdot e^{-0.75(t-0.4)} + 105\cdot (t-0.4)\cdot (-0.75)\cdot e^{-0.75(t-0.4)} \\ \\ &= 105\cdot e^{-0.75(t-0.4)}\cdot\bigl(1-0.75(t-0.4)\bigr) \\ \\ &= 105\, e^{-0.75(t-0.4)}\,(1.3-0.75t)\end{aligned}\] Om een extremum te vinden lossen we de vergelijking \(C'(t)=0\) op: omdat de exponentiële functie positief is, moet gelden dat \(1.3-0.75t =0\) oftewel \(t\approx 1.7\). Na pakweg 1 uur en drie kwartier is de plasmaconcentratie maximaal.

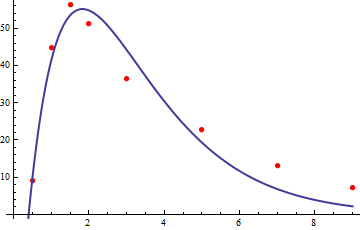
Dit is overigens geen fictief voorbeeld want onderstaande grafiek toont de grafiek van deze functie samen met metingen van de plasmaconcentratie op de achtergrond die afkomstig zijn uit een studie over plasmaconcentraties na orale toediening van propranolol, simultaan met een intraveneuze toediening [Bron: Olanoff, L., et. al. (1986). Clinical Pharmacology and Therapeutics, 40, 408-414]. Het getal \(0.4\) dat in deze formule steeds in combinatie met de tijd \(t\) voor komt is de geschatte vertragingstijd voor het farmacon bij orale toediening, d.w.z. de tijd nodig voordat het farmacon om van de maag in de dunne darm terecht te komen om vervolgens geabsorbeerd te worden via de poortader. Als we de tijdschaal opschuiven naar dit tijdstip en hier de oorsprong \(t=0\) vastleggen, dan zou de formule voor de plasmaconcentratie vereenvoudigen tot \(C(t)=105\, t\, e^{-0.75t}\), maar veel maakt dit voor de berekening van het maximum niet uit.