Differentials and integrals: Applications of integration
 Volume of a soldid of revolution
Volume of a soldid of revolution
We consider the graph of a function \(y=f(x)\) that is continuous and nonnegative on an interval \([a,b]\). The region bounded by the graph of \(f\), the \(x\)-axis, and the lines \(x=a\) and \(x=b\) can now be revolved about the \(x\)-axis and in this way a solid of revolution \(S\) is created. You can just as well rotate the graph of \(f\) about the \(x\)-axis and bound it by means of the vertical planes through the points \((a,0,0)\) and \((b,0,0)\).
In the left figure below, only a quarter of \(S\) is sketched (with \(x\ge0,y\ge 0\) and \(z\ge 0\). In the right figure below, the solid of revolution is sketched that you get by rotating the sine graph on the interval \([0,2\pi]\) about the \(x\) axis. An interactive version showing the solid of revolution of the function \(f(x)=x^2-3x\) on the interval \([1,3]\) is also available. You can show and rotate the graph of the function, adjust the interval by moving the points \(A\) and \(B\), and change the 3D-viewpoint with the right mouse button.
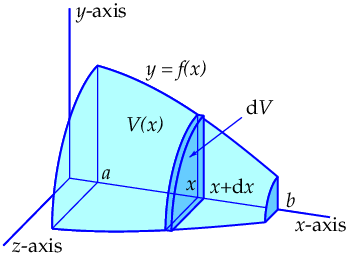
The volume of a solid of revolution obtained by revolving the region under the graph of a function about the x-axis Choose a number \(x\) on the interval \([a,b]\) and let \(V(x)\) be the volume of the portion of the solid of revolution to the left of the vertical plane through \((x,0,0)\). Then \(V(a)=0\) and \(V(b)=\textrm{volume of the solid of revolution }S\). For a small increment \(\dd x\) the increment \(V(x+\dd x)-V(x)\) is equal to the volume of the thin slice of the solid of revolution between the vertical planes through the points \((x,0,0)\) and \((x+\dd x,0,0)\). For a very small (mathematicians say 'infinitesimally small') increment \(\dd x\) this is almost equal to the volume of a cylindrical disk with radius \(f(x)\) and thickness \(\dd x\). The volume of this cylindrical disc is equal to the product of the area of the circle with radius \(f(x)\) and the thickness \(\dd x\), i.e., it is equal to \(\pi\cdot \bigl(f(x)\bigr)^2\,\dd x\). The expression \(\pi\cdot \bigl(f(x)\bigr)^2\,\dd x\) is a differential and equal to the \(\dd V\) differential of the volume function. So: \(\dd V=\pi \cdot \bigl(f(x)\bigr)^2\,\dd x\).
The requested volume of the solid of revolution \(S\) that is obtained by revolving the area bounded by the graph of the function \(f\), the \(x\)-axis and the lines \(x=a\) and \(x=b\) around the \(x\)-axis, is equal to \[\begin{aligned}\text{volume of }S&=V(b)\\[0.25cm]&=\int_a^b \pi\cdot\bigl(f(x)\bigr)^2\,\dd x\\[0.25cm]&=\pi\int_a^b\bigl(f(x)\bigr)^2\,\dd x\end{aligned}\]
\[\begin{aligned}V(S) &=\pi \int_1^3\bigl(f(x)\bigr)^2\,\dd x\\[0.25cm] &=\pi\int_{1}^{3}(x^2-3x)^2\,\dd x\\[0.25cm]
&=\pi\int_1^3(x^4-6x^3+9x^2)\,\dd x\\[0.25cm] &=\pi\cdot\Bigl[\frac{1}{5}x^5-\frac{3}{2}x^4+3x^3\Bigr]_1^3\\[0.25cm] &=\pi\cdot\Bigl(\bigl(\frac{3^5}{5}-\frac{3^5}{2}+3^4\bigr)-\bigl(\frac{1}{5}-\frac{3}{2}+3\bigr)\Bigr)\\[0.25cm] &=\pi\cdot\bigl(\frac{81}{10}-\frac{17}{10}\bigr)\\[0.25cm] &=\frac{32}{5}\pi\end{aligned}\]
\(\phantom{xabc}\)
Instead of rotation about the \(x\)-axis, you can also rotate part of a graph of a function around the \(y\)-axis. Also in this case, the volume of the solid of revolution can be calculated. We just need to swap the roles of \(x\) and \(y\). So we should describe the curve as \(x=f(y)\) instead of \(y=f(x)\). and the limits must be given in terms of \(y\), as in the figure below from \(y=c\) to \(y=d\).
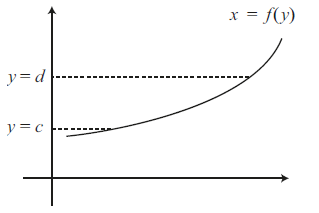
The requested volume of the solid of revolution is then equal to \(\pi\int_c^d f(y)^2\,\dd y\).
The part of the parabola \(y=x^2+1\) defined over the positive \(x\)-axis can also be described as \(x=\sqrt{y-1}\). We can rotate the planar region \(R\) bounded by the parabola, the \(y\)-axis and the horizontal lines \(y=2\) and \(y=5\) about the \(y\)-axis. See the figure below.
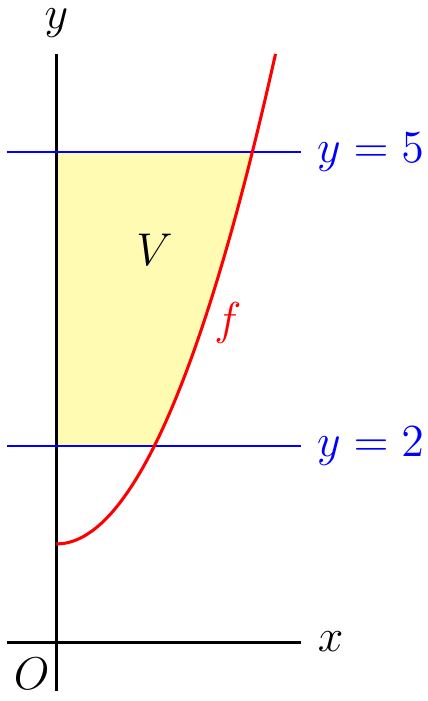
Calculate the volume \(V(S)\) of the so-obtained solid of revolution \(S\).
\[\begin{aligned}I(L)&=\pi \int_{2}^{5}\bigl(x(y)\bigr)^2\,\dd y\\[0.25cm] &=\pi \int_{^2}^{5} \bigl(\sqrt{y-1}\bigr)^2\,\dd y\\[0.25cm] &=\pi \int_{2}^{5} (y-1)\,\dd y\\[0.25cm] &=\pi \int_{1}^{4}u\,\dd u& \blue{u=y-1, \dd u=\dd y}\\[0.25cm] &=\pi \cdot\Bigl[\frac{1}{2}u^2\Bigr]_{1}^{4}\\[0.25cm] &=\pi\cdot\Bigl(\frac{4^2}{2}-\frac{1^2}{2}\Bigr)\\[0.25cm]&=\frac{17}{2}\pi\end{aligned}\]
\(\phantom{abc}\)
We return to a region under the graph of a continuous nonnegative function \(f\). Instead of revolving the region \(R\) under the graph about a \(x\)-axis, you can also rotate such a region around the \(y\)-axis.
The volume of a solid of revolution obtained by revolving the region of the plane under the graph of a function about the y-axis Choose a number \(x\) in the interval \([a,b]\) and let \(V(x)\) be the volume of the portion of the solid of revolution to the left of the vertical plane through \((x,0,0)\) obtained by revolving about the \(y\)-axis. Then \(V(a)=0\) and \(V(b)=\textrm{volume of the solid of revolution }S\). For a small increment \(\dd x\) the increment \(V(x+\dd x)-V(x)\) is equal to the volume of the thin slice of the solid of revolution between the vertical planes through the points \((x,0,0)\) and \((x+\dd x,0,0)\). For very small (mathematicians say 'infinitesimally small') increment \(\dd x\) this is almost equal to the volume of a cylindrical shell with radius \(x\), thickness \(\dd x\) and height \(f(x)\). The volume of this cylindrical shell is equal to the product of the circumference of a circle with radius \(x)\), the height \(f(x)\) and the thickness \(\dd x\), i.e., it equals \(2\pi x\, f(x)\,\dd x\). This expression is a differential and equal to the \(\dd V\) differential of the volume function. So: \(\dd V=2\pi x\, f(x)\,\dd x\).
The requested volume of the solid of revolution \(S\), which is obtained by revolving the region bounded by the graph of the function \(f\), the \(x\)-axis and the lines \(x=a\) and \(x=b\) about the \(y\)-axis, is equal to \[\begin{aligned}\text{volume of }S &=V(b)\\[0.25cm]&=2\pi \int_a^b x\,f(x)\,\dd x\end{aligned}\]
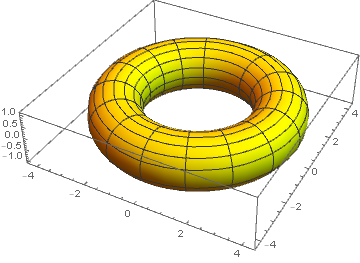
The equation of a circle with radius \(r\) and center \((c,0)\) is given by the equation \[(x-c)^2+y^2=r^2\] The semicircle above the positive \(x\)-axis is then the graph of the function \[f(x)=\sqrt{r^2-(x-c)^2}\] with \[c-r\le x \le c+r\] To calculate the volume of the torus, we double the volume of the solid of revolution that is obtained by revolving the area under the graph of the function \(f\) about the \(y\)-axis. \[\begin{aligned}\text{volume of the torus } &=2\cdot 2\pi \int_{c-r}^{c+r}x\,f(x)\,\dd x\\[0.25cm] &=4\pi \int_{c-r}^{c+r}x\,\sqrt{r^2-(x-c)^2}\,\dd x\\[0.25cm]
&=4\pi \int_{-r}^{r}(u+c)\sqrt{r^2-u^2}\,\dd u\\ &\phantom{abcdwxyzabcdwxyz} \blue{u=x-c, \dd u=\dd x}\\[0.25cm]
&=4\pi \int_{-r}^{r}u\,\sqrt{r^2-u^2}\,\dd u + 4\pi \,c\int_{-r}^{r}\sqrt{r^2-u^2}\,\dd u\\[0.25cm]
&=4\pi \,c\int_{-r}^{r}\sqrt{r^2-u^2}\,\dd u \\ &\phantom{abcdwxyzabcdwxyz} \blue{\text{because }u\,\sqrt{r^2-u^2}\text{ is an odd funtion}}\\[0.25cm]
&=4\pi\,c \int_{\pi}^{0}-r^2\sin^2z\,\dd z\\ &\phantom{abcdwxyzabcdwxyz} \blue{u=r\cos{z}, \dd u=-r\sin{z}\, \dd z}\\[0.25cm]
&=4\pi\,c\,r^2 \int_{0}^{\pi}\sin^2z\,\dd z\\[0.25cm]
&=4\pi\,c\,r^2\cdot\frac{1}{2}\left( \int_{0}^{\pi}\sin^2z\,\dd z+\int_{0}^{\pi}\cos^2z\,\dd z\right)
\\[0.25cm]
&=2\pi\,c\,r^2 \int_{0}^{\pi}\bigl(\sin^2z+\cos^2z\bigr)\,\dd z \\[0.25cm]
&=2\pi\,c\,r^2\int_{0}^{\pi}1\,\dd z\\[0.25cm]
&=2\pi\,c\,r^2\,\pi \\[0.25cm]
&=2\pi^2r^2c\end{aligned}\]
\(\phantom{abc}\)
Finally, we give the formulas for the volume of a solid of revolution by rotating a region under a parametric curve about the \(x\)- or \(y\)-axis.
The volume of a solid of revolution obtained by revolving a region under the curve about the x- or y-axis When you revolve a parametric curve \(\bigl(x(t),y(t)\bigr)\) on the interval \([a,b]\) about the \(x\)- or \(y\)-axis, then the volume \(V\) of the solid of revolution obtained by revolving the region under the curve or to the left of the curve is given by the formulas below.
Rotation about the \(x\)-axis
\[V=\pi\int_a^b y(t)^2\cdot\frac{\dd x}{\dd t}\,\dd t\]
Rotation about the \(y\)-axis
\[V=\pi\int_a^b x(t)^2\cdot\frac{\dd y}{\dd t}\,\dd t\]