Differentialen en integralen: Toepassingen van integratie
 Inhoud van een omwentelingslichaam
Inhoud van een omwentelingslichaam
We gaan uit van de grafiek van een functie \(y=f(x)\) die continu en niet-negatief is op een interval \([a,b]\). Het vlakdeel dat wordt ingesloten door de grafiek van \(f\), de \(x\)-as, en de lijnen \(x=a\) en \(x=b\) kunnen we nu rond de \(x\)-as te wentelen en op deze manier komt een omwentelingslichaam \(L\) tot stand. Net zo goed kun je de grafiek van \(f\) wentelen om de \(x\)-as en begrenzen d.m.v. de verticale vlakken door de punten \((a,0,0)\) en \((b,0,0)\).
In de linkerfiguur hieronder is slechts een kwart gedeelte van \(L\) geschetst (met \(x\ge0,y\ge 0\) en \(z\ge 0\). In de rechterfiguur hieronder is het omwentelingslichaam geschets dat je krijgt door de sinusgrafiek op het interval \([0,2\pi]\) rond de \(x\)-as te wentelen. Een interactieve versie die het omwentelingslichaam bij de functie \(f(x)=x^2-3x\) op het interval \([1,3]\) is ook beschikbaar. Je kunt hierin de grafiek van de functie roteren, het interval aanpassen door de punten \(A\) en \(B\) te verplaatsen, en het 3D-gezichtspunt via de rechtermuisknop veranderen.
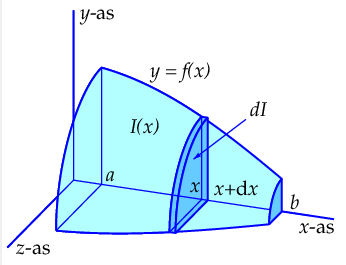
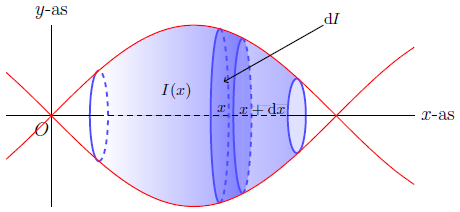
De inhoud van een omwentelingslichaam verkregen door wenteling van het vlakdeel onder de grafiek van een functie om de x-as Kies een getal \(x\) in het interval \([a,b]\) en laat \(I(x)\) de inhoud zijn van het gedeelte van het omwentelingslichaam links van het verticale vlak door \((x,0,0)\). Dan geldt dat \(I(a)=0\) en \(I(b)=\textrm{inhoud van omwentelingslichaam }L\). Voor een kleine toename \(\dd x\) is de toename \(I(x+\dd x)-I(x)\) gelijk aan de inhoud van het dunne plakje van het omwentelingslichaam tussen de verticale vlakken door de punten \((x,0,0)\) en \((x+\dd x,0,0)\). Voor zeer kleine (wiskundigen zeggen infinitesimaal kleine) toename \(\dd x\) is dit nagenoeg gelijk aan de inhoud van een cylinderschijf met straal \(f(x)\) en dikte \(\dd x\). De inhoud van deze cylinderschijf is gelijk aan het product van de oppervlakte van de cirkel met straal \(f(x)\) en de dikte \(\dd x\), dat wil zeggen gelijk is aan \(\pi\cdot \bigl(f(x)\bigr)^2\,\dd x\). De uitdrukking \(\pi\cdot \bigl(f(x)\bigr)^2\,\dd x\) is een differentiaal en gelijk aan de differentiaal \(\dd I\) van de inhoudsfunctie. Dus: \(\dd I=\pi \cdot \bigl(f(x)\bigr)^2\,\dd x\).
De gevraagde inhoud van het omwentelingslichaam \(L\) dat ontstaat door het vlakdeel ingesloten door de grafiek van de functie \(f\), de \(x\)-as en de lijnen \(x=a\) en \(x=b\) te wentelen om de \(x\)-as is gelijk aan \[\begin{aligned}\text{inhoud van }L&=I(b)\\[0.25cm]&=\int_a^b \pi\cdot\bigl(f(x)\bigr)^2\,\dd x\\[0.25cm]&=\pi\int_a^b\bigl(f(x)\bigr)^2\,\dd x\end{aligned}\]
\[\begin{aligned}I(S) &=\pi \int_1^3\bigl(f(x)\bigr)^2\,\dd x\\[0.25cm] &=\pi\int_{1}^{3}(x^2-3x)^2\,\dd x\\[0.25cm]
&=\pi\int_1^3(x^4-6x^3+9x^2)\,\dd x\\[0.25cm] &=\pi\cdot\Bigl[\frac{1}{5}x^5-\frac{3}{2}x^4+3x^3\Bigr]_1^3\\[0.25cm] &=\pi\cdot\Bigl(\bigl(\frac{3^5}{5}-\frac{3^5}{2}+3^4\bigr)-\bigl(\frac{1}{5}-\frac{3}{2}+3\bigr)\Bigr)\\[0.25cm] &=\pi\cdot\bigl(\frac{81}{10}-\frac{17}{10}\bigr)\\[0.25cm] &=\frac{32}{5}\pi\end{aligned}\]
\(\phantom{xabc}\)
In plaats van wentelen om de \(x\)-as, kun je een deel van een grafiek van een functie ook wentelen om de \(y\)-as. Ook dan kan de inhoud van het omwentelingslichaam berekend worden. We moeten alleen de rollen van \(x\) en \(y\) verwisselen. We moeten dus de kromme beschrijven als \(x=f(y)\) in plaats van \(y=f(x)\). en de grenzen moeten in termen van \(y\) gegeven worden, zoals in onderstaande figuur van \(y=c\) tot \(y=d\).
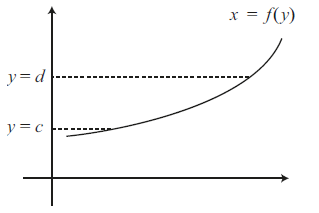
De gevraagde inhoud van het omwentelingslichaam is dan gelijk aan \(\pi\int_c^d f(y)^2\,\dd y\).
Het gedeelte van de parabool \(y=x^2+1\) gedefinieerd over de positieve \(x\)-as kun je ook beschrijven via \(x=\sqrt{y-1}\). We kunnen het vlakdeel \(V\) begrensd door de parabool, de \(y\)-as en de horizontale lijnen \(y=2\) en \(y=5\) wentelen om de \(y\)-as. Zie onderstaande figuur.
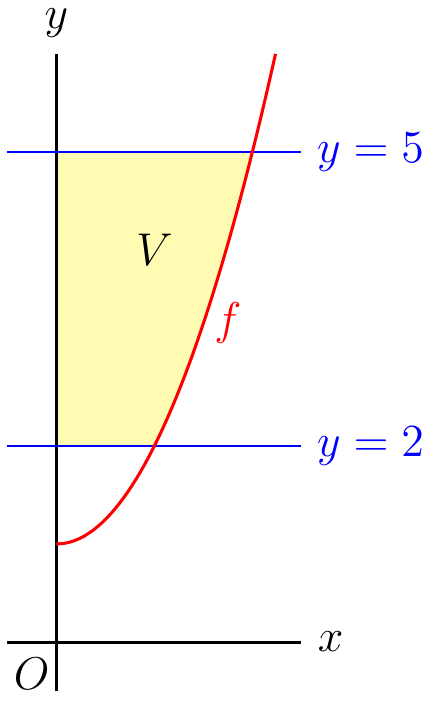
Reken de inhoud \(I(L)\) van het zo verkregen omwentelingslichaam \(L\) exact uit.
\[\begin{aligned}I(L)&=\pi \int_{2}^{5}\bigl(x(y)\bigr)^2\,\dd y\\[0.25cm] &=\pi \int_{^2}^{5} \bigl(\sqrt{y-1}\bigr)^2\,\dd y\\[0.25cm] &=\pi \int_{2}^{5} (y-1)\,\dd y\\[0.25cm] &=\pi \int_{1}^{4}u\,\dd u& \blue{u=y-1, \dd u=\dd y}\\[0.25cm] &=\pi \cdot\Bigl[\frac{1}{2}u^2\Bigr]_{1}^{4}\\[0.25cm] &=\pi\cdot\Bigl(\frac{4^2}{2}-\frac{1^2}{2}\Bigr)\\[0.25cm]&=\frac{17}{2}\pi\end{aligned}\]
\(\phantom{abc}\)
Keren we terug naar een vlakdeel onder de grafiek van een continue niet-negatieve functie \(f\). In plaats van het wentelen van het vlakdeel \(V\) onder de grafiek om een \(x\)-as, kun je zo'n vlakdeel ook wentelen om de \(y\)-as.
De inhoud van een omwentelingslichaam verkregen door wenteling van het vlakdeel onder de grafiek van een functie om de y-as Kies een getal \(x\) in het interval \([a,b]\) en laat \(I(x)\) de inhoud zijn van het gedeelte van het omwentelingslichaam links van het verticale vlak door \((x,0,0)\) door wenteling om de \(y\)-as. Dan geldt dat \(I(a)=0\) en \(I(b)=\textrm{inhoud van omwentelingslichaam }L\). Voor een kleine toename \(\dd x\) is de toename \(I(x+\dd x)-I(x)\) gelijk aan de inhoud van het dunne plakje van het omwentelingslichaam tussen de verticale vlakken door de punten \((x,0,0)\) en \((x+\dd x,0,0)\). Voor zeer kleine (wiskundigen zeggen infinitesimaal kleine) toename \(\dd x\) is dit nagenoeg gelijk aan de inhoud van een cylindervormige schil met straal \(x\), dikte \(\dd x\) en hoogte \(f(x)\). De inhoud van deze cylindervormige schil is gelijk aan het product van de omtrek van een cirkel met straal \(x)\), de hoogte \(f(x)\) en de dikte \(\dd x\), dat wil zeggen gelijk is aan \(2\pi x\, f(x)\,\dd x\). Deze uitdrukking is een differentiaal en gelijk aan de differentiaal \(\dd I\) van de inhoudsfunctie. Dus: \(\dd I=2\pi x\, f(x)\,\dd x\).
De gevraagde inhoudvan het omwentelingslichaam \(L\) dat ontstaat door het vlakdeel ingesloten door de grafiek van de functie \(f\), de \(x\)-as en de lijnen \(x=a\) en \(x=b\) te wentelen om de \(y\)-as is gelijk aan \[\begin{aligned}\text{inhoud van }L &=I(b)\\[0.25cm]&=2\pi \int_a^b x\,f(x)\,\dd x\end{aligned}\]
De vergelijking van een cirkel met straal \(r\) en centrum \((c,0)\) wordt gegeven door de vergelijking \[(x-c)^2+y^2=r^2\] De halve cirkel boven de positieve \(x\)-as is dan de grafiek van de functie \[f(x)=\sqrt{r^2-(x-c)^2}\] met \[c-r\le x \le c+r\] Om de inhoud van de torus te berekenen verdubbelen we de inhoud van het omwentelingslichaam dat verkregen wordt het vlakdeel onder de grafiek van de functie \(f\) te wentelen om de \(y\)-as. \[\begin{aligned}\text{Inhoud van de torus } &=2\cdot 2\pi \int_{c-r}^{c+r}x\,f(x)\,\dd x\\[0.25cm] &=4\pi \int_{c-r}^{c+r}x\,\sqrt{r^2-(x-c)^2}\,\dd x\\[0.25cm]
&=4\pi \int_{-r}^{r}(u+c)\sqrt{r^2-u^2}\,\dd u\\ &\phantom{abcdwxyzabcdwxyz} \blue{u=x-c, \dd u=\dd x}\\[0.25cm]
&=4\pi \int_{-r}^{r}u\,\sqrt{r^2-u^2}\,\dd u + 4\pi \,c\int_{-r}^{r}\sqrt{r^2-u^2}\,\dd u\\[0.25cm]
&=4\pi \,c\int_{-r}^{r}\sqrt{r^2-u^2}\,\dd u \\ &\phantom{abcdwxyzabcdwxyz} \blue{\text{want }u\,\sqrt{r^2-u^2}\text{ is oneven functie}}\\[0.25cm]
&=4\pi\,c \int_{\pi}^{0}-r^2\sin^2z\,\dd z\\ &\phantom{abcdwxyzabcdwxyz} \blue{u=r\cos{z}, \dd u=-r\sin{z}\, \dd z}\\[0.25cm]
&=4\pi\,c\,r^2 \int_{0}^{\pi}\sin^2z\,\dd z\\[0.25cm]
&=4\pi\,c\,r^2\cdot\frac{1}{2}\left( \int_{0}^{\pi}\sin^2z\,\dd z+\int_{0}^{\pi}\cos^2z\,\dd z\right)
\\[0.25cm]
&=2\pi\,c\,r^2 \int_{0}^{\pi}\bigl(\sin^2z+\cos^2z\bigr)\,\dd z \\[0.25cm]
&=2\pi\,c\,r^2\int_{0}^{\pi}1\,\dd z\\[0.25cm]
&=2\pi\,c\,r^2\,\pi \\[0.25cm]
&=2\pi^2r^2c\end{aligned}\]
\(\phantom{abc}\)
Tot slot geven we nog de formules voor de inhoud van een omwentelingslichaam door een vlakdeel onder een geparametriseerde kromme te wentelen om de \(x\)- of \(y\)-as.
De inhoud van een omwentelingslichaam verkregen door wenteling van het vlakdeel onder de kromme om de x- of y-as Wanneer je een kromme die in parametervorm \(\bigl(x(t),y(t)\bigr)\) op het interval \([a,b]\) gedefinieerd is wentelt om de \(x\)- of \(y\)-as, dan wordt de inhoud \(I(L)\) van het omwentelinglichaam \(L\) verkregen door het vlakdeel onder de kromme of links van de kromme gegeven door onderstaande formules.
Wenteling om \(x\)-as
\[I(L)=\pi\int_a^b y(t)^2\cdot\frac{\dd x}{\dd t}\,\dd t\]
Wenteling om \(y\)-as
\[I(L)=\pi\int_a^b x(t)^2\cdot\frac{\dd y}{\dd t}\,\dd t\]