Differentials and integrals: Applications of integration
 Surface area of a solid of revolution
Surface area of a solid of revolution
We consider the graph of a function \(y=f(x)\) that is differentiable and nonegative on an interval \([a,b]\). We rotate the graph about the \(x\)-axis, but now look at the surface area of the solid of revolution. This solid of revolution is generally not equal to that of the solid of revolution obtained by rotating the region under the graph; this latter solid of revolution generally has vertical planar sections through the points \((a,0,0)\) and \((b,0,0)\). Now It is only about the surface that is obtained by rotating the graph.
Surface area of a solid of revolution obtained by revolving the graph of a nonegative differentiable function about the x-axis Choose a number \(x\) in the interval \([a,b]\) and let \(A(x)\) be the area of the part of the solid of revolution to the left of the vertical plane through \((x,0,0)\). Then \(A(a)=0\) and \(A(b)=\textrm{surface area of the solid of revolution }L\). For a small increment \(\dd x\) the increment \(A(x+\dd x)-A(x)\) is equal to the area of the thin band of the solid of revolution between the vertical planes through the points \((x,0,0)\) and \((x+\dd x,0,0)\). See the figure below.
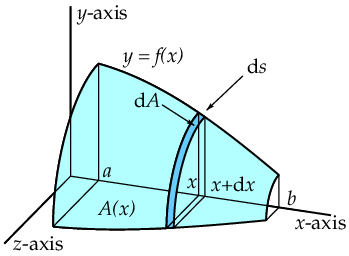
Since the left edge of the band is a circle wih radius \(f(x)\), its circumference is \(2\pi f(x)\). So we still need to determine the width \(\dd s\) of the band to compute its surface area. For very small (mathematicians say 'infinitesimally small') increment \(\dd x\) we almost have a straight line segment \(\dd s\) and the area of the band is equal to \(2\pi f(x)\cdot \dd s\). The line segment \(\dd s\) has length \[\sqrt{\dd x^2+\dd f^2}=\sqrt{\dd x^2+\bigl(f'(x)\,\dd x\bigr)^2}=\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\] The expression \(2\pi f(x)\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\) is a differential and equal to the differential \(\dd A\) of the area function. So: \(\dd A=2\pi f(x)\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\).
The requested surface area of the solid of revolution \(S\), which is obtained by revolving the graph of the function \(f\) on the interval \([a,b]\) about the \(x\)-axis, is equal to \[\begin{aligned}\text{surface area of }S&=A(b)\\[0.25cm]&=\int_a^b 2\pi f(x)\,\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\\[0.25cm]&=2\pi\int_a^bf(x)\,\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\end{aligned}\]
In a similar way, the formula for the surface area of a rotation about the \(y\)-axis can be derived.
Surface area of a field of revolution obtained by revolving the graph of a nonegative differentiable function about the y-axis The surface area of the solid of revolution \(S\) obtained by revolving the graph of a nonegative differentiable function \(f\) on the interval \([a,b]\) about the \(y\)-axis is equal to \[\begin{aligned}\text{surface area of }S=2\pi\int_a^b x\,\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\end{aligned}\]
Finally, we give the formulas for the surface area of a solid of revolution by revolving a parametric curve about the \(x\)- or \(y\)-axis.
Surface area of a solid of revolution obtained by revolving a parametric curve about the \(x\)- or \(y\)-axis When a parametic curve \(\bigl(x(t),y(t)\bigr)\) on the interval \([a,b]\) is revolved about the \(x\)- or \(y\)-axis, then the surface area \(A(S)\) of the solid revolution \(S\) can be computed by the formulas below.
Rotation about the \(x\)-axis
\[A(S)=2\pi\int_a^b y(t)\sqrt{\bigl(x'(t)\bigr)^2+\bigl(y'(t)\bigr)^2}\,\dd t\]
Rotation about the \(y\)-axis
\[A(S)=2\pi\int_a^b x(t)\sqrt{\bigl(x'(t)\bigr)^2+\bigl(y'(t)\bigr)^2}\,\dd t\]


