Oppervlakte van een omwentelingslichaam verkregen door wenteling van de grafiek van een niet-negatieve differentieerbare ffunctie om de x-as Kies een getal \(x\) in het interval \([a,b]\) en laat \(O(x)\) de oppervlakte zijn van het gedeelte van het omwentelingslichaam links van het verticale vlak door \((x,0,0)\). Dan geldt dat \(O(a)=0\) en \(O(b)=\textrm{oppervlakte van omwentelingslichaam }L\). Voor een kleine toename \(\dd x\) is de toename \(O(x+\dd x)-O(x)\) gelijk aan de oppervlakte van de dunne band van het omwentelingslichaam tussen de verticale vlakken door de punten \((x,0,0)\) en \((x+\dd x,0,0)\). Zie onderstaande figuur.

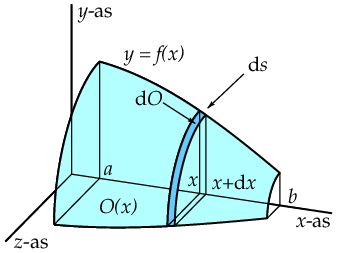
Omdat de linkerrand van de band een cirkel met straal \(f(x)\) is, is de omtrek hiervan gelijk aan \(2\pi f(x)\). We moeten dus nog de breedte \(\dd s\) van de band bepalen om de oppervlakte hiervan te kunnen berekenen. Voor zeer kleine (wiskundigen zeggen infinitesimaal kleine) toename \(\dd x\) is \(\dd s\) nagenoeg gelijk aan een recht lijnstukje en is de oppervlakte van de band gelijk aan \(2\pi f(x)\cdot \dd s\). Het lijnstukje \(\dd s\) heeft de lengte \[\sqrt{\dd x^2+\dd f^2}=\sqrt{\dd x^2+\bigl(f'(x)\,\dd x\bigr)^2}=\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\] De uitdrukking \(2\pi f(x)\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\) is een differentiaal en gelijk aan de differentiaal \(\dd O\) van de oppervlaktefunctie. Dus: \(\dd O=2\pi f(x)\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\).

De gevraagde oppervlakte van het omwentelingslichaam \(L\) dat ontstaat door de grafiek van de functie \(f\) op het interval \([a,b]\) te wentelen om de \(x\)-as is gelijk aan \[\begin{aligned}\text{oppervlakte van }L&=O(b)\\[0.25cm]&=\int_a^b 2\pi f(x)\,\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\\[0.25cm]&=2\pi\int_a^bf(x)\,\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\end{aligned}\]

Oppervlakte van een omwentelingslichaam verkregen door wenteling van de grafiek van een niet-negatieve differentieerbare functie om de y-as De oppervlakte van het omwentelingslichaam \(L\) dat ontstaat door de grafiek van een niet-negatieve differentieerbare functie \(f\) op het interval \([a,b]\) te wentelen om de \(y\)-as is gelijk aan \[\begin{aligned}\text{oppervlakte van }L=2\pi\int_a^b x\,\sqrt{1+\bigl(f'(x)\bigr)^2}\dd x\end{aligned}\]

Oppervlakte van een omwentelingslichaam verkregen door wenteling van een geparametriseerde kromme om de x- of y-as Wanneer je een kromme die in parametervorm \(\bigl(x(t),y(t)\bigr)\) op het interval \([a,b]\) gedefinieerd is wentelt om de \(x\)- of \(y\)-as, dan wordt de oppervlakte \(O(L)\) van het omwentelingslichaam \(L\) verkregen door onderstaande formules.