Differentials and integrals: Applications of integration
 Line integral of a function
Line integral of a function
So far we have interpreted an integral of a function \(f(x)\) over an interval \([a,b]\) as the area under the graph of \(f\). As an application, you can view this in three-dimensional space as the total area of a thin fence that is along the \(x\) axis and has \(f(x)\) height at every point \((x,0)\) in the \(xy\) plane.
But why should we limit ourselves to a perfectly straight fence? Can the fence not be placed just as well along a curve \(\mathcal{C}\) in the \(xy\)-plane? We must now describe the height with a function in two variables, say \(f(x,y)\), where the point \((x,y)\) must always lie on the curve \(\mathcal{C}\); see the figure below.
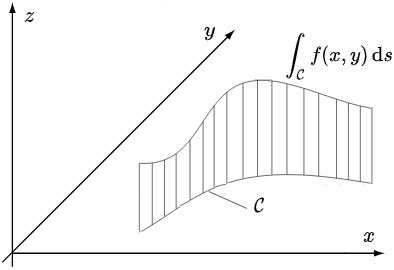
A second consequence is that we can no longer use the differential \(\dd x\) in the integration process. But as we have seen with the topic Length of a curve, we can also use the length increase \(\dd L\) along the curve as a small piece to calculate the height for. We have already found mathematical expressions for this. More common, and also seen in the figure above, is to use the increase in distance traveled along the curve, with the symbol \(\dd s\). This is only a minor change in language and notation, but since it is written in that way in most textbooks, we will include that in this theory page. Using the Riemann sum as an approximation of the integral we are looking for, we get the following definitions of a line integral for a neat function \(f\), denoted \(\displaystyle\int_\mathcal{C} f\,\dd s\), where \(f\) denotes \(f(x,y)\) with \((x,y)\) a point on \(\mathcal{C}\). The curve \(\mathcal{C}\) is also called the path of integration.
Line integral of a function Let \(\mathcal{C}\) be a planar parametric curve described by two differentiable coordinate functions \(x=x(t), y=y(t)\) through a parameter \(t\) in an interval \([a,b]\); we speak of a smooth curve. Suppose \(f(x,y)\) is a 'neat' function, at least on \(\mathcal{C}\). Then the line integral from point \(A=\bigl(x(a),y(a)\bigr)\) to point \(B=\bigl(x(b),y(b)\bigr)\) is given by \[\int_\mathcal{C}f(x,y)\,\dd s=\int_a^b f\bigl(x(t),y(t)\bigr)\sqrt{\bigl(x'(t)\bigr)^2+\bigl(y'(t)\bigr)^2}\,\dd t\]
\[\begin{aligned}\cv{x(t)\\ y(t)} &= \cv{2 \\ 2}+t\cdot\left(\cv{0 \\ -2}-\cv{2 \\ 2}\right)\\[0.25cm] &= \cv{2 \\ 2} + t\cdot \cv{-2 \\ -4}\\[0.25cm] &= \cv{2-2\,t\\ 2-4\,t}\end{aligned}\] where \(t\in[0,1]\). Along this path the line integral can be calculated as follows: \[\begin{aligned}\int_C y^3\,\dd s &= \int_{0}^{1} \left(2-4\,t\right)^3\sqrt{(-2)^2+(-4)^2}\,\dd t\\[0.25cm] &=\int_{0}^{1} 2\,\sqrt{5}\,\left(2-4\,t\right)^3\,\dd t\\[0.25cm] &= \Biggl[-{{\sqrt{5}\,\left(2-4\,t\right)^4}\over{8}}\Biggr]_{0}^{1}\\[0.25cm] &= -2\sqrt{5}+2\sqrt{5} \\[0.25cm] &= 0\end{aligned}\]
Line integral along a piecewise defined curve A line integral can also be defined for a curve \(\mathcal{C}\) that consists of contiguous segments of smooth curves, say \(\mathcal{C}_1, \mathcal{C}_2, \ldots, \mathcal{C}_n\). The line integral of a 'neat' function \(f(x,y)\) over the piecewise defined curve \(\mathcal{C}\) can then be calculated as follows: \[\int_\mathcal{C}f(x,y)\,\dd s=\int_\mathcal{C_1}f(x,y)\,\dd s + \int_\mathcal{C_2}f(x,y)\,\dd s+ \cdots + \int_\mathcal{C_n}f(x,y)\,\dd s\]
Alternative line integrals We have used the distance travelled \(s\) as variable for integration in the above definition. This is most commonly used in applications, for example in classical mechanics to determine the work done to move an object along a given path or to determine the center of gravity of a thin curved wire. But actually, other variables such as \(x\) and \(y\) can also be used as variables of integration. Then you get line integrals of type \[\int_{\mathcal{C}} f(x,y)\,\dd x\quad\text{and}\quad \int_{\mathcal{C}} f(x,y)\,\dd y\] The line integral \(\displaystyle \int_{\mathcal{C}} f(x,y)\,\dd s\) represents the area below the surface \(z=f(x,y)\) but above the curve \(\mathcal{C}\). The integrals \(\displaystyle \int_{\mathcal{C}} f(x,y)\,\dd x\) and \(\displaystyle \int_{\mathcal{C}} f(x,y)\,\dd y\) represent the area of the projection of this region on the \(xz\)-plane and the \(yz\)-plane, respectively; see the figure below:
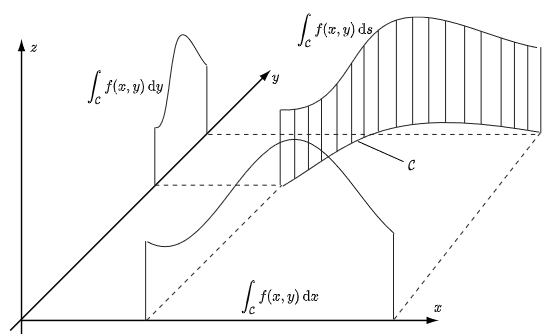
The combination of the two alternative line integrals for two smooth functions \(f(x,y)\) and \(g(x,y)\) is also common in practice: \[\int_{\mathcal{C}}f(x,y)\,\dd x + g(x,y)\,\dd y\] An example: suppose that \(\mathcal{C}\) is the curve \(y=x^2\) from \((0,0)\) to \((1,1)\), then: \[\begin{aligned}\int_{\mathcal{C}}x^2y\,\dd x + x\,y^2\,\dd y &= \int_{0}^{1} \left(x^2y+\,y^2\,\frac{\dd y}{\dd x}\right)\dd x\\[0.25cm] &= \int_{0}^{1} \left(x^4+2x^6\right)\,\dd x\\[0.25cm] &= \int_{0}^{1} \biggl[\frac{1}{5}x^5+\frac{1}{3}x^6\biggr]_{0}^{1}\\[0.25cm] &= \frac{1}{5}+\frac{1}{3}\\[0.25cm] &= \frac{7}{15}\end{aligned}\] Actually, in this case, we are not talking about a line integral of a function anymore, but about a line integral of a differential form. We will see in vector calculus that there are more types of line integrals.
The concept of line integral of a function can also be extended to three-dimensional space.
Line integral Suppose \(\mathcal{C}\) is a parametric curve in three-dimensional space described by three differentiable coordinate functions \(x=x(t), y=y(t), z=z(t)\) through a parameter \(t\) in an interval \([a,b]\). Suppose \(f(x,y)\) is a 'neat' function, at least on \(\mathcal{C}\). Then the line integral between the points \(A=\bigl(x(a),y(a), z(a)\bigr)\) and \(B=\bigl(x(b),y(b), z(b)\bigr)\) is given by \[\int_\mathcal{C}f(x,y,z)\,\dd s=\int_a^b f\bigl(x(t),y(t),z(t)\bigr)\sqrt{\bigl(x'(t)\bigr)^2+\bigl(y'(t)\bigr)^2+ \bigl(z'(t)\bigr)^2}\,\dd t\]
\(\bar{z}={}\) \( \dfrac{2\pi}{ \ln(1+2\pi)}-1\)
In fact, we are asked to calculate the following line integral: \[\int_{\mathcal{C}} z\cdot \rho(x,y,z)\,\dd s\] Due to the parameterisation we can compute the total mass \(M\) of the wire in the following way: \[\begin{aligned}M &=\int_{\mathcal{C}} \rho(x,y,z)\,\dd s\\[0.25cm] &= \int_{\mathcal{C}} \rho\bigl(x(t),y(t),z(t)\bigr)\cdot \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi} \frac{1}{1+t}\sqrt{(-\sin t)^2+\cos^2t+1^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi} \frac{1}{1+t} \sqrt{\sin^2t+\cos^2t+1^2}\,\dd t\\[0.25cm] &= \sqrt{2} \int_{0}^{2\pi} \frac{1}{1+t}\,\dd t\\[0.25cm] &= \sqrt{2} \biggl[\ln(1+t)\biggr]_{0}^{2\pi} \\[0.25cm] &= \sqrt{2}\bigl(\ln(1+2\pi)-\ln(1)\bigr)\\[0.25cm] &= \sqrt{2}\ln(1+2\pi)\end{aligned}\] For the calculation of the \(z\)-coordinate of the centre of gravity we need the so-called static moment \(M_{xy}\). Here, the density function plays the role of a weighting factor in the integration of the vertical coordinate along the spiral: \[\begin{aligned}M_{xy} &= \int_{\mathcal{C}} z\cdot \rho(x,y,z)\,\dd s\\[0.25cm] &= \int_{\mathcal{C}} z(t)\cdot \rho\bigl(x(t),y(t,)z(t)\bigr)\cdot \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi}t\cdot \frac{1}{1+t}\sqrt{(-\sin t)^2+\cos^2t+1^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi}t\cdot \frac{1}{1+t}\sqrt{\sin^2t+\cos^2t+1^2}\\[0.25cm] &= \sqrt{2}\int_{0}^{2\pi}\frac{t}{1+t}\,\dd t\\[0.25cm] &= \sqrt{2}\int_{0}^{2\pi}\left(1-\frac{1}{1+t}\right)\dd t\\[0.25cm] &= \sqrt{2}\cdot \biggl[t-\ln(1+t)\biggr]_{0}^{2\pi} \\[0.25cm] &= \sqrt{2}\Bigl(\bigl(2\pi-\ln(1+2\pi)\bigr)-\bigl(0-\ln(1)\bigr)\Bigr)\\[0.25cm] &= \sqrt{2}\bigl(2\pi-\ln(1+2\pi)\bigr)\end{aligned}\]
The vertical coordinate \(\bar{z}\) of the centre of gravity is then: \[\begin{aligned}\bar{z} &= \frac{M_{xy}}{M} \\[0.25cm] &= \frac{\sqrt{2}\bigl(2\pi-\ln(1+2\pi)\bigr)}{ \sqrt{2}\ln(1+2\pi)}\\[0.25cm] &= \frac{2\pi}{ \ln(1+2\pi)}-1\\[0.25cm] &\approx 2.164 \end{aligned}\] The approximated value of the exact result shows that the vertical coordinate of the centre of gravity is less than the value \(\pi\) for a spiral with a constant density. This is consistent with the expectation that the centre of gravity is at lower height for a density that decreases with height.


