We consider the following concrete example of an area calculation: The request is to calculate the area of the region enclosed by the \(x\) axis and the graph of the function \(f(x)=1-x^2.\) This can be done via an approach similar to the method discussed in the previous section, in the example of the area calculation of a circle via differentials.

Let \(O(x)\) be the the area of the region enclosed by the \(x\)-axis, the vertical line through the point \((x,0)\) and the graph of \(f(x)\). In the original problem one is asked to compute \(O(1).\) For a small increment \(dx\) the difference \(O(x+\dd x)-O(x)\) is equal to the area of the region enclosed by the \(x\)-axis, the vertical lines through points \((x,0)\) and \((x+\dd x,0)\), and the graph of \(f(x)\). This is illustrated in the figure below.

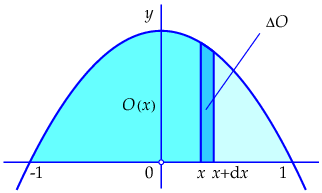
The extra narrow strip that has been added can be approximated for small \(\dd x\) by the rectangular strip of width \(\dd x\) and height \(f(x)\) as shown in the figure below.

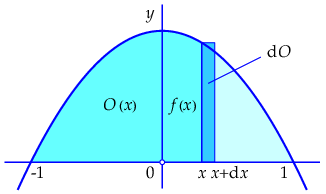
The area of the narrow rectangle is in this case equal to \((1-x^2)\,\dd x.\) This is actually for infinitesimal \(\dd x\) nothing else than the differential of the function \(O(x)\). Thus: \[\dd O=(1-x^2)\,\dd x.\] The right-hand side can also be written as \(\dd(x-\tfrac{1}{3}x^3).\) But if differentials of two functions are equal to each other then these functions differ only a constant. So, in this case we get: \[O(x)=x-\tfrac{1}{3}x^3+c,\] for a certain constant \(c\). This constant is fixed by the requirement that \(O(-1)=0.\)
Consequently \(c=\tfrac{2}{3}.\) But then: \(O(1)=1\!\tfrac{1}{3}\). Note that for the function \(O(x)\) the following equality is valid: \(O\,'(x)=(1-x^2).\)