We bekijken het volgende concrete voorbeeld van een oppervlakteberekening: gevraagd wordt de oppervlakte te berekenen van het gebied ingesloten door de \(x\)-as en de grafiek van de functie \(f(x)=1-x^2.\) Dit kan met een aanpak die lijkt op de methode besproken in de vorige sectie in het voorbeeld van de oppervlakteberekening van een cirkel via differentialen.

Laat \(O(x)\) de oppervlakte zijn van het gebied ingesloten door de \(x\)-as, de verticale lijn door het punt \((x,0)\) en de grafiek van \(f(x)\). In het oorspronkelijke probleem wordt gevraagd \(O(1).\) Voor een kleine toename \(\dd x\) is de toename \(O(x+\dd x)-O(x)\) gelijk aan de oppervlakte van het gebied ingesloten door de \(x\)-as, de verticale lijnen door de punten \((x,0)\) en \((x+\dd x,0)\), en de grafiek van \(f(x)\). Dit wordt in onderstaande figuur geïllustreerd.

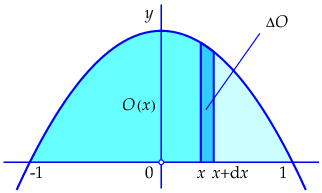
De extra smalle strook die erbij gekomen is kan benaderd worden voor kleine \(\dd x\) met de rechthoekige strook met breedte \(\dd x\) en hoogte \(f(x)\) zoals getoond in onderstaande figuur.

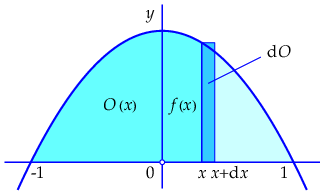
De oppervlakte van de smalle rechthoek is in dit geval gelijk aan \((1-x^2)\,\dd x.\) Dit is eigenlijk voor verwaarloosbare \(\dd x\) niets anders dan de differentiaal van de functie \(O(x)\). Dus: \[\dd O=(1-x^2)\,\dd x.\] Het rechterlid kan ook geschreven worden als \(\dd(x-\tfrac{1}{3}x^3).\) Maar als differentialen van twee functies gelijk aan elkaar zijn dan verschillen deze functies slecht een constante van elkaar. Dus geldt in dit geval: \[O(x)=x-\tfrac{1}{3}x^3+c,\] voor zekere constante \(c\). Deze constante wordt vastgelegd door de eis dat \(O(-1)=0.\)
Hieruit volgt dat \(c=\tfrac{2}{3}.\) Maar dan geldt: \(O(1)=1\!\tfrac{1}{3}\). Merk op dat voor de functie \(O(x)\) geldt dat \(O\,'(x)=(1-x^2).\)