De eerdere aanpak van een oppervlakteberekening laat zich veralgemeniseren tot een berekening van de oppervlakte van een gebied ingesloten door de \(x\)-as, twee verticale lijnen met vergelijkingen \(x=a\) en \(x=b\), en de grafiek van een functie \(f(x).\) Laat \(F(x)\) een functie zijn met \(F'(x)=f(x)\), dan heet \(F(x)\) een primitieve functie van \(f(x).\) Zo'n primitieve functie is niet uniek bepaald: voor elke constante \(c\) is de functie \(G(x)=F(x)+c\) ook een primitieve functie van \(f(x)\).

Laat \(O(x)\) de oppervlakte zijn van het gebied ingesloten door de \(x\)-as, de verticale lijnen door de punten \((a,0)\) en \((x,0)\), en de grafiek van \(f(x)\). Onderstaande figuur illustreert deze situatie.

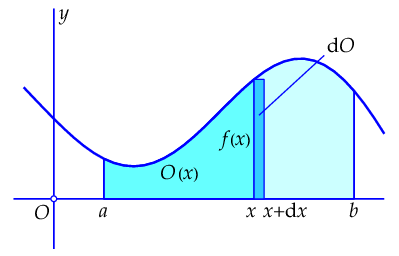
Net als in het concrete voorbeeld kan men dan kijken naar de toename \(O(x+\dd x)-O(x)\), d.w.z. de oppervlakte van het gebied ingesloten door de \(x\)-as, de verticale lijnen door de punten \((x,0)\) en \((x+\dd x,0)\), en de grafiek van \(f(x)\), voor kleine toename \(\dd x.\) Als voorheen kan de extra smalle strook die erbij gekomen is benaderd worden voor kleine \(\dd x\) met een rechthoekige strook met breedte \(\dd x\) en hoogte \(f(x)\). Dit is eigenlijk voor verwaarloosbare \(\dd x\) niets anders dan de differentiaal van de functie \(O(x)\). Dus: \[\dd O=f(x)\,\dd x.\] Met andere woorden: \[O\,'(x)=f(x).\] Dus is de functie \(O(x)\) een primitieve functie van \(f(x)\) en op een constante na gelijk aan \(F(x).\) Omdat \(O(a)=0\) moet gelden dat \(O(x)=F(x)-F(a).\) In het bijzonder is \(O(b)=F(b)-F(a).\) Dit getal \(F(b)-F(a)\) heet de bepaalde integraal van de functie \(f(x)\) over het gesloten interval \([a,b]\) en men hanteert de volgende notatie: \[\int_a^b f(x)\,\dd x=F(b)-F(a).\] De functie \(f(x)\) noemt men de integrand en het teken \(\int_{}^{}\) dat voor de differentiaal \(f(x)\,\dd x\) staat heet het integraalteken. Dit teken is bedacht door Leibniz, een van de pioniers op het gebied van differentiaal- en integraalrekening.

Overigens, de integratievariabele \(x\), die meestal een plaats aanduidt, speelt geen enkele speciale rol in bovenstaande berekening en kan door iedere andere nog beschikbare letter worden vervangen, bijvoorbeeld door de letter \(t\) die meestal gereserveerd wordt voor tijd. De context van de integraalberekening wijzigt, maar de berekening zelf blijft in essentie gelijk.

In plaats van \(F(b)-F(a)\) wordt vaak \(\bigl[F(x)\bigr]^b_a\) of \(\bigl[F(x)\bigr]^{x=b}_{x=a}\) geschreven. Dus:
\[\int_a^bf(x)\,\dd x=\bigl[F(x)\bigr]^b_a = F(b)-F(a)\text.\]