In the earlier explanation of area and primitive function we secretly assumed that \(f(x)\ge 0\) all \(x\) in \([a,b]\). But what to do when the function \(f(x)\) also attains negative values?

If \(f(x)\le 0\) for all \(x\) in \([a,b]\), then \(-f(x)\ge 0\) and the function \(O_{-f}(x)\) that represents the area of the region enclosed by the \(x\)-axis, the vertical line through the point \((x,0)\) and graph of \(-f(x)\) is a primitive function of \(-f(x)\). This is illustrated in the figure below.

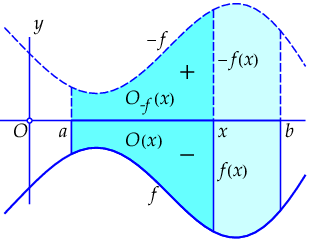
Because \(O\,'_{-f}(x)=-f(x)\), then in turn \(O(x)=-O_{-f}(x)\) is a primitive function of \(f(x)\). But this is also the area on \([a,x]\) between the horizontal \(x\)-axis and the graph of \(f(x)\) with an additional minus sign. If the area of a plane region below the horizontal axis is considered a negative quantity, then \(\int_a^b f(x)\,\dd x\) still represents the area between the \(x\)-axis, the graph of \(f(x)\) and the vertical lines through \((a,0)\) and \((b,0)\).

If \(f(x)\) changes sign on \([a,b]\), positive and negative contributions must be combined. For regions where the function values are negative, the contributions to the area must be taken with a minus. In the figure below, there exist on the interval two regions with a positive contribution and one region with a negative contribution to the area.

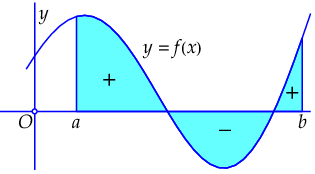
In this interpretation of area, the following statement remains true: