In de eerdere uitleg over oppervlakte en primitieve functie is stiekem verondersteld dat \(f(x)\ge 0\) voor alle \(x\) in \([a,b]\). Maar wat te doen als de functie \(f(x)\) ook negatieve waarden aanneemt?

Als \(f(x)\le 0\) voor alle \(x\) in \([a,b]\), dan is \(-f(x)\ge 0\) en is de functie \(O_{-f}(x)\) die de oppervlakte van het gebied ingesloten door de \(x\)-as, de verticale lijn door het punt \((x,0)\) en de grafiek van \(-f(x)\) voorstelt een primitieve functie van \(-f(x)\). Dit wordt geïllustreerd in onderstaande figuur.

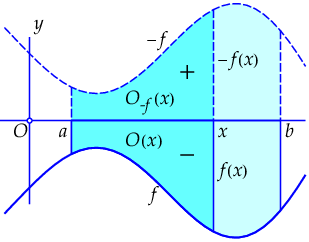
Omdat \(O\,'_{-f}(x)=-f(x)\), is dan \(O(x)=-O_{-f}(x)\) op zijn beurt een primitieve functie van \(f(x)\). Maar dit is tevens de oppervlakte op \([a,x]\) tussen de horizontale \(x\)-as en de grafiek van \(f(x)\) voorzien van een minteken. Als de oppervlakte van een vlakdeel onder de horizontale als negatief geteld wordt, dan stelt \(\int_a^b f(x)\,\dd x\) dus nog steeds de oppervlakte tussen de \(x\)-as, de grafiek van \(f(x)\) en de verticale lijnen door \((a,0)\) en (\(b,0)\) voor.

Als \(f(x)\) op \([a,b]\) van teken wisselt, moeten positieve en negatieve bijdragen met elkaar gecombineerd worden. Voor vlakdelen waar de functiewaarden negatief zijn moeten de oppervlaktes dus negatief meegeteld worden. In onderstaande figuur zijn er op het interval twee vlakdelen met een positieve bijdrage en één vlakdeel met een negatieve bijdrage aan de oppervlakte.

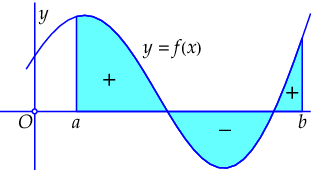
In deze interpretatie van oppervlakte blijft dus de volgende bewering waar: