Parametric curves: Plane curves
 Plane curves
Plane curves
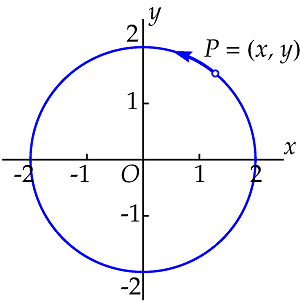
The circle on the right-hand side , with the origin \(O=(0,0)\) as centre and with radius \(2\), consists of all points \(P(x,y)\) such that \(x^2+y^2=4\).
But the points on the circle can also be described by a parametric curve, for which we specify the points on the curve via the coordinate functions \(x=2\cos t\) and \(y=2\sin t\). We speak of coordinate functions because the coordinates \(x\) and \(y\) are functions of the variable \(t\). As \(t\) increases from \(0\) to \(2\pi\), the point \(P\) moves counter clockwise along the circle.
\(\phantom{xxx}\)
In the interactive diagram below the figure you can move the point \(P\) by dragging the slider between \(0\) and \(2\pi\); the turquoise arc indicates the path along which the point \(P=(2\cos t,2\sin t)\) travels from \(0\) to \(t\).
In general, you can describe a plane curve mathematically by two functions \(x=f(t)\) and \(y=g(t)\) describe a curve in the plane; we speak of a parameterisation or parameter equations of the curve with parameter \(t\). Almost always one uses neat functions \(f\) and \(g\) as coordinate functions. The parameter \(t\) represents time in many applications.
The parameterisation of a curve is not unique: the following example illustrates a new parameterisation of the circle with origin \(O=(0,0)\) as centre and with radius \(2\).
parameterisations of a circle Parameter equations of the circle with the origin \(O=(0,0)\) as centre and with radius \(2\) is: \[x=2\cos t\quad\text{and}\quad y=2\sin t\] Another parameterisation of the circle is: \[x=2\sin t\quad\text{and}\quad y=2\cos t\] The direction of circulation is now clockwise, and at \(t=0\) the point is \((0,2)\).
Yet another parameterisation of the circle is: \[x=2(1-t^2)\quad\text{and}\quad 2t\sqrt{2-t^2}\qquad\text{for}\quad -\sqrt{2}\le t\le \sqrt{2}\] After all, the following is true for this parameterisation: \[\begin{aligned}x^2+y^2&= 4(1- t^2)^2+ 4t^2(2-t^2)\\[0.25cm] &= 4(1- 2t^2+t^4)+ 4t^2(2-t^2)\\[0.25cm] &=4\end{aligned}\]
A fourth parameterisation of the circle, but now without the point \((-2,0)\), uses rational functions as a coordinate functions: \[x=\frac{2-2t^2}{1+t^2}\quad\text{and}\quad y=\frac{4t}{1+t^2}\] This is not a parameterisation of the circle because the point \((-2,0)\) cannot be described in this way; but otherwise all points on the circle are present! After all, the following is true for this parameterisation: \[\begin{aligned}x^2+y^2&= \frac{(2-2t^2)^2}{(1+t^2)^2}+\frac{(4t)^2}{(1+t^2)^2}\\[0.25cm] &= \frac{4-8t^2+4t^4}{(1+t^2)^2}+\frac{16t^2}{(1+t^2)^2}\\[0.25cm] &= \frac{4+8t^2+4t^4}{(1+t^2)^2}\\[0.25cm] &=\frac{4(1+t^2)^2}{(1+t^2)^2} \\[0.25cm] &= 4\end{aligned}\]


