Krommen in het vlak

Geparametriseerde krommen: Krommen in het vlak

Krommen in het vlak

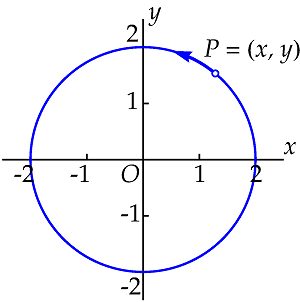
De hiernaast getekende cirkel, met de oorsprong $O=(0,0)$ als middelpunt en met straal $2$ , bestaat uit alle punten $P(x,y)$ waarvoor geldt dat $x^2+y^2=4$ .

Maar de punten op de cirkel kunnen we ook beschrijven via een geparametriseerde kromme of parameterkromme, waarbij we de punten specificeren door de coördinaatfuncties $x=2\cos t$ en $y=2\sin t$ . We spreken van coördinaatfuncties omdat de coördinaten $x$ en $y$ functies zijn van de variabele $t$ . Als $t$ van $0$ naar $2\pi$ loopt, doorloopt het punt $P$ de cirkel in de pijlrichting.

$\phantom{xxx}$

In het interactieve diagram onder de figuur is het punt $P$ te verplaatsen door de schuifbalk tussen $0$ en $2\pi$ te bewegen; de turquoise boog geeft aan welk pad het punt $P=(2\cos t,2\sin t)$ al van $0$ naar $t$ heeft afgelegd.

GeoGebra

In het algemeen kun je door twee functies $x=f(t)$ en $y=g(t)$ een kromme in het vlak beschrijven; we spreken dan van een parametrisatie of parametervorm van de kromme met parameter $t$ . Bijna altijd neemt men daarbij 'nette' functies $f$ en $g$ als coördinaatfuncties. De parameter $t$ stelt in veel toepassingen de tijd voor.

De parametrisatie van een kromme is niet uniek: het volgende voorbeeld illustreert een nieuwe parametrisatie van de cirkel met de oorsprong $O=(0,0)$ als middelpunt en met straal $2$ .

Een parametervorm van de cirkel met de oorsprong $O=(0,0)$ als middelpunt en met straal $2$ is:

$x=2\cos t\quad\text{en}\quad y=2\sin t$ Een tweede gelijksoortige parametrisatie van de cirkel is:

$x=2\sin t\quad\text{en}\quad y=2\cos t$ De omlooprichting is nu met de wijzers van de klok mee en bij $t=0$ hoort het punt $(0,2)$ .

Een derde parametrisatie van de cirkel is:

$x=2(1-t^2)\quad\text{en}\quad y=2t\sqrt{2-t^2}\qquad\text{met}\quad -\sqrt{2}\le t\le \sqrt{2}$ Voor deze parametrisatie geldt immers:

$\begin{aligned}x^2+y^2&= 4(1- t^2)^2+ 4t^2(2-t^2)\\[0.25cm] &= 4(1- 2t^2+t^4)+ 4t^2(2-t^2)\\[0.25cm] &=4\end{aligned}$

Een vierde parametrisatie van de cirkel, maar nu zonder het punt $(-2,0)$ , hanteert rationale functies als coördinaatfuncties:

$x=\frac{2-2t^2}{1+t^2}\quad\text{en}\quad y=\frac{4t}{1+t^2}$ Dit is geen parametrisatie van de cirkel omdat het punt $(-2,0)$ niet beschreven kan worden op deze manier; maar verder doen alle punten op de cirkel mee! Voor deze parametrisatie geldt immers:

$\begin{aligned}x^2+y^2&= \frac{(2-2t^2)^2}{(1+t^2)^2}+\frac{(4t)^2}{(1+t^2)^2}\\[0.25cm] &= \frac{4-8t^2+4t^4}{(1+t^2)^2}+\frac{16t^2}{(1+t^2)^2}\\[0.25cm] &= \frac{4+8t^2+4t^4}{(1+t^2)^2}\\[0.25cm] &=\frac{4(1+t^2)^2}{(1+t^2)^2} \\[0.25cm] &= 4\end{aligned}$