Parametric curves: Polar coordinates and polar curves
 Polar coordinates
Polar coordinates
Polar coordinates If a rectangular coordinate system \(Oxy\) is chosen in a plane, then the location of a point \(P\) in that plane can be described by coordinates \((x,y)\). But the location of a point \(P\) in the plane different from the origin \(O\) can also be characterized by its distance \(r\) to the origin, and the angle \(\varphi\) that the segment \(OP\) makes with the positive \(x\)-axis (see the figure below). The pair \((r,\varphi)\) form the polar coordinates of point \(P\). Unlike rectangular coordinates, polar coordinates are not unique: you can always add an integer multiple of \(2\pi\) to the angle \(\varphi\). The origin is called the pole and the positive \(x\)-axis is called the polar axis.
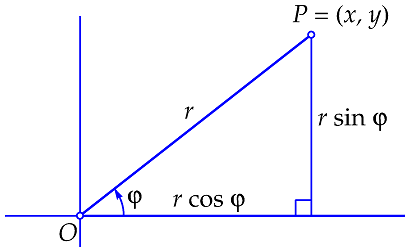
Conversion It is easy to compute rectangular coordinates \((x,y)\) of a point from polar coordinates \((r,\varphi)\) of that point: \[x=r\cos(\varphi)\quad\text{and}\quad y=r\sin(\varphi)\] Conversely, you can compute polar coordinates \((r,\varphi)\) from rectangular coordinates \((x,y)\) of that point through the relations \[r=\sqrt{x^2+y^2}\quad\text{and}\quad \tan(\varphi)=\frac{y}{x}\;\;\;(\text{provided }x\neq 0)\] You can solve the latter equation via the inverse arctangent function: \(\varphi=\arctan\left(\frac{y}{x}\right)\) if \(x>0\) and \(\varphi=\arctan\left(\frac{y}{x}\right)+\pi\) if \(x<0\). If \(x=0\), then you can take \(\varphi=\tfrac{1}{2}\pi\) for positive \(y\) and \(\varphi=-\tfrac{1}{2}\pi\) for negative \(y\).
Some curves in the plane can be easily be described by a relationship between \(r\) and \(\varphi\); this is called a polar representation of a curve.
An Archimedean spiral An Archimedean spiral is given by the equation \(r=a+b\cdot \varphi\), where \(a\) and \(b\) are positive numbers that define the starting point and spacing of the spiral. Below the curve is drawn for \(r=2+\tfrac{1}{5}\varphi\) where \(\varphi\ge -10\) in order to avoid being confronted with a negative radius \(r\). The points on the curve with parameter value \(\varphi=-\tfrac{4}{3}\pi\) and \(\varphi=0\) are marked.
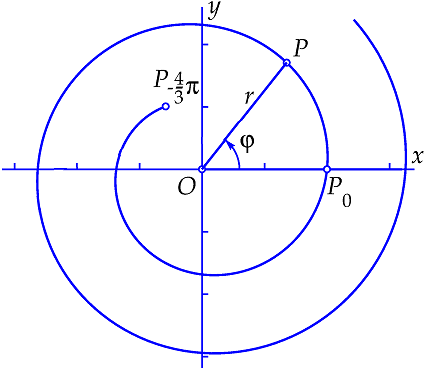
Interactive version of an Archimean spiral
In the interactive diagram below you can explore the Archimedean spiral. We have created this diagram in such manner that it can also be used for other curves expressed in polar coordinates. Have, for example, a look at the curve with equation \(r=2-2\cos(\tfrac{1}{2}\varphi)\) with \(\varphi\in[0,4\pi]\) (for \(\varphi\) you can enter phi).
Look at some more examples of polar representations of curves and the conversion from polar coordinates to normal coordinates, and vice versa.
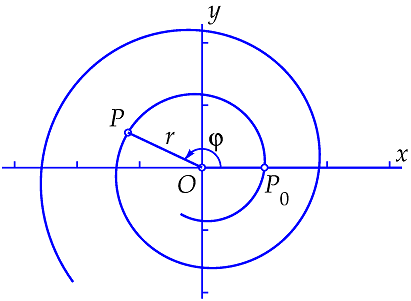
The equation of the logarithmic spiral can also be written as \(r=e^{c\cdot\varphi}\).
So we have in rectangular coordinates \((x,y)\): \[P(x,y)=\bigl(r\cos(\varphi),r\sin(\varphi)\bigr)=\bigl(e^{c\cdot\varphi}\cos(\varphi),e^{c\varphi}\sin(\varphi)\bigr)\]


