Geparametriseerde krommen: Poolcoördinaten
 Poolcoördinaten
Poolcoördinaten
Poolcoödinaten Als in het vlak een \(Oxy\)-coördinatenstelsel gegeven is, kan de positie van een punt \(P\) in het vlak door de \((x,y)\)-coördinaten beschreven worden. Maar de positie van een punt \(P\) in het vlak verschillend van de oorsprong \(O\) kun je dan ook weergeven door zijn afstand \(r\) tot de oorsprong en de hoek \(\varphi\) die de verbindingslijn \(OP\) maakt met de positieve \(x\)-as (zie onderstaande figuur). De getallen \(r\) en \(\varphi\) vormen samen de poolcoördinaten van punt \(P\). Poolcoördinaten zijn in tegenstelling tot gewone coördinaten niet uniek: je kunt bij de hoek altijd een geheel veelvoud van \(2\pi\) optellen. De oorsprong noemt men de pool en de positieve \(x\)-as heet de poolas.
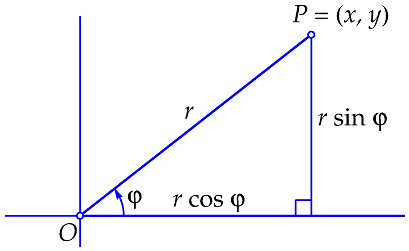
Conversie Uit gegeven poolcoördinaten \((r,\varphi)\) kun je gemakkelijk de gewone coördinaten bereken: \[x=r\cos\varphi\quad\mathrm{en}\quad y=r\sin\varphi\] Omgekeerd, kun je uit gegeven coördinaten \((x,y)\) de bijpassende poolcoördinaten afleiden door de verbanden \[r=\sqrt{x^2+y^2}\quad\text{en}\quad \tan\varphi=\frac{y}{x}\quad(\text{ mits }x\neq 0)\] De laatste vergelijking kan je oplossen m.b.v. de arctangens functie. Als \(x=0\), dan kun je \(\varphi=\tfrac{1}{2}\pi\) nemen voor positieve \(y\) en \(\varphi=-\tfrac{1}{2}\pi\) voor negatieve \(y\).
Sommige krommen in het vlak zijn gemakkelijk te beschrijven door een verband tussen \(r\) en \(\varphi\); dit heet ook wel een poolvoorstelling van een kromme.
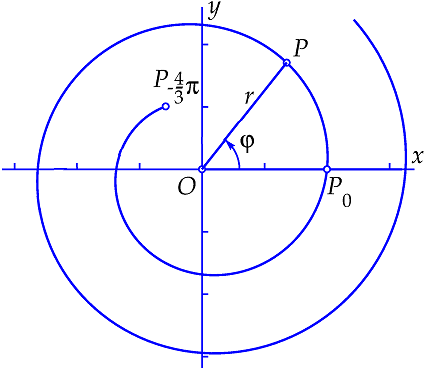
Archimedes-spiraal Een Archimedes-spiraal wordt gegeven door de vergelijking \(r=a+b\cdot \varphi\), waarbij \(a\) en \(b\) positieve getallen zijn die het beginpunt en spatiëring van de spiraal vastleggen. Hieronder staat de kromme getekend voor \(r=2+\tfrac{1}{5}\!\varphi\), waarbij \(\varphi\ge -10\) om te voorkomen dat we met een negatieve straal \(r\) te maken krijgen. De punten op de kromme met parameterwaarde \(\varphi=-\tfrac{4}{3}\pi\) en \(\varphi=0\) zijn gemarkeerd.
Interactieve versie van een Archimedes-spiraal
In onderstaand interactief diagram kun je bovenstaande Archimedes-spiraal exploreren. We heb dit diagram zo gemaakt deze deze ook bruikbaar is voor andere krommen die uitgedrukt zijn in poolcoördinaten. Kijk bijvoorbeeld ook maar eens naar de kromme met vergelijking \(r=2-2\cos(\tfrac{1}{2}\varphi)\) met \(\varphi\in[0,4\pi]\) (voor \(\varphi\) kun je phi intoetsen).
Bekijk nog een paar voorbeelden van poolvoorstellingen van krommen en conversie van poolcoördinaten naar gewone coördinaten.
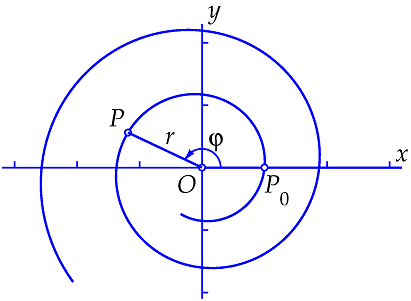
De vergelijking van de logaritmische spiraal kan ook geschreven worden als \(r=e^{c\cdot\varphi}\).
Dus in gewone coördinaten hebben we: \[P(x,y)=\bigl(r\cos(\varphi),r\sin(\varphi)\bigr)=\bigl(e^{c\cdot\varphi}\cos(\varphi),e^{c\varphi}\sin(\varphi)\bigr)\]


