Parametric curves: Space curves
Parametric curves in space
The lower-left spiral consists of all the points \(P(x,y,z)\) specified by the coordinate functions \[\left\{\;\begin{aligned} x &= \cos(8\pi t)\\ y &= \sin(8\pi t)\\ z &= t\end{aligned}\right.\] We speak of coordinate functions because the coordinates \(x\), \(y\) and \(z\) are functions of the variable \(t\). As \(t\) increases from \(-1\) to \(1\), the point \(P\) spirals counter clockwise in the upward direction, starting in \(P_{-1}=(1,0,-1)\) and terminating in \(P_1=(1,0,1)\).
The lower-right diagram is interactive; drag the right-mouse button to look at it from a different perspective or give it with the right-mouse button a push to animate the objects.
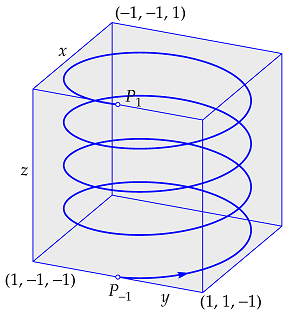
In general, you can describe a space curve mathematically by three functions \[\left\{\;\begin{aligned} x &= f(t)\\ y &= g(t)\\ z&= h(t)\end{aligned}\right.\] We speak of a parameterisation or parameter equations of the curve with parameter \(t\). Almost always one uses neat functions \(f, g\) and \(h\) as coordinate functions. The parameter \(t\) represents time in many applications.
The parameterisation of a curve in the space is not unique: thus the spiral in the above example, may also be parametrized by \[\left\{\;\begin{aligned}x &= \cos(2t^3)\\ y &= \sin(2t^3)\\ z &= t^3\end{aligned}\right.\] with the \(t\)-domain again equal to the interval \(-1\le t\le 1\). The only thing that has changed is the way the point \(P\) moves along the curve as \(t\) increases from \(-1\) to \(1\).
