Geparametriseerde krommen: Krommen in de ruimte
Geparametriseerde krommen in de ruimte
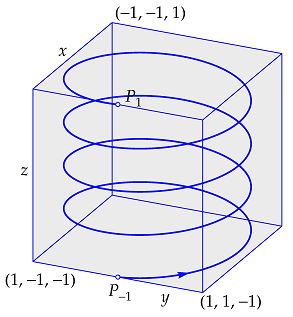
De linksonder getekende spiraal bestaat uit alle punten \(P(x,y,z)\) die gespecificeerd zijn door de coördinaatfuncties \[\left\{\;\begin{aligned} x &= \cos(2t)\\ y &= \sin(2t)\\ z &= t\end{aligned}\right.\] We spreken van coördinaatfuncties omdat de coördinaten \(x\), \(y\) en \(z\) functies zijn van de variabele \(t\). Als \(t\) van \(-1\) naar \(1\) loopt, doorloopt het punt \(P\) de spiraal in de pijlrichting, startend in \(P_{-1}=(1,0,-1)\) en eindigend in \(P_1=(1,0,1)\).
Het diagram rechtsonder is interactief: sleep met de rechter-muisknop om het geheel vanuit een ander perspectief te bekijken of geef de figuur een 'duwtje' om een animatie van de objecten te krijgen.
In het algemeen kun je door drie functies \[\left\{\;\begin{aligned} x &= f(t)\\ y &= g(t)\\ z&= h(t)\end{aligned}\right.\] een kromme in de ruimte beschrijven; we spreken dan van een parametrisatie of parametervorm van de kromme met parameter \(t\). Bijna altijd neemt men daarbij 'nette' functies als coördinaatfuncties. De parameter \(t\) stelt in veel toepassingen de tijd voor.
De parametrisatie van een kromme in de ruimte is niet uniek: zo kan de spiraal in bovenstaand voorbeeld ook geparametriseerd worden door \[\left\{\;\begin{aligned}x &= \cos(2t^3)\\ y &= \sin(2t^3)\\ z &= t^3\end{aligned}\right.\] met als \(t\) -domein weer het interval \(-1\le t\le 1\). Het enige wat verandert is de manier waarop het punt \(P\) beweegt over de kromme wanneer van \(-1\) naar \(1\) loopt.
