Trigonometry: Trigonometric functions
Trigonometry in arbitrary triangles
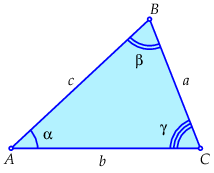
Let \(ABC\) be an arbitrary triangle with angles \(\alpha\), \(\beta\) and \(\gamma\) at vertices \(A\), \(B\) and \(C\), sides of length \(a\), \(b\) and \(c\) opposite to \(A\), \(B\) and \(C\), and area \(O\). The figure on the right-hand side shows the situation for a triangle with only acute angles.
For this situation we will discuss two relationships between the lengths of the sides and the angles and we will determine an area formula, which by the way is also correct if one of the angles of the triangle is obtuse.
sine rule \[\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}\]
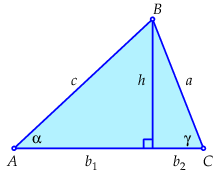
Suppose that the length of the altitude from \(B\) to the opposite side \(AC\) is equal to \(h\), as in the figure on the right-hand side with only acute angles and \(b=b_1+b_2\). Then \(h=c\sin(\alpha)\) and \(h=a\sin(\gamma)\). So: \(c\sin(\alpha)=c\sin(\gamma)\), or \(\frac{a}{\sin(\alpha)}=\frac{c}{\sin(\gamma)}\). The other relationships in the sine rule can be proved in a similar way.
For the situation with an obtuse angle, say \(\gamma\), one can also draw an altitude from \(B\), but the point at distance \(h\) is on the extension of the line segment \(AC\). This poses no problem for the proof of the sine rule when one applies \(\sin(\pi-\gamma)=\sin(\gamma)\).
cosine rule \[\begin{aligned} a^2 &= b^2+c^2-2bc\cos(\alpha)\\[0.25cm]
b^2 &= a^2+c^2-2ac\cos(\beta)\\[0.25cm] c^2 &= a^2+b^2-2ab\cos(\gamma)\end{aligned}\]
Suppose that the length of the altitude from \(B\) to the opposite side \(AC\) is equal to \(h\), as in the figure on the right-hand side with only acute angles and \(b=b_1+b_2\). Then, according to the Pythagorean theorem, \(c^2=b_1^2+h^2\) and \(a^2=b_2^2+ h^2\). So: \[\begin{aligned} c^2&=b_1^2+a^2-b_2^2\\[0.25cm] &= (b-b_2)^2+a^2-b_2^2\\[0.25cm] &=a^2+b^2-2b_2b\\[0.25cm] & a^2+b^2-2ab\cos(\gamma)\end{aligned}\] The other versions of the cosine rule are proved in a similar way.
For the situation with an obtuse angle, say \(\gamma\), one can also draw an altitude from \(B\), but the point at distance \(h\) is on the extension of the line segment \(AC\). This poses no problem for the proof of the cosine rules when one applies \(\cos(\pi-\gamma)=-\cos(\gamma)\).
Area formula \[O=\tfrac{1}{2}bc\sin(\alpha)=\tfrac{1}{2}ac\sin(\beta)=\tfrac{1}{2}ab\sin(\gamma)\]
Suppose that the length of the altitude from \(B\) to the opposite side \(AC\) is equal to \(h\), as in the figure on the right-hand side with only acute angles and \(b=b_1+b_2\). Then: \(O=\tfrac{1}{2}bh\) and \(h=c\sin(\alpha)\). So: \(O=\tfrac{1}{2}bc\sin(\alpha)\). The other relations for the area of a triangle can be proved in a similar way.
For the situation with an obtuse angle, say \(\gamma\), one can also draw an altitude from \(B\), but the point at distance \(h\) is on the extension of the line segment \(AC\). This poses no problem for the proof of the area formula when one applies \(\sin(\pi-\gamma)=\sin(\gamma)\).
