Goniometrische functies en hun inversen: Goniometrische functies
Goniometrie in willekeurige driehoeken
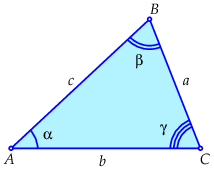
Stel dat \(ABC\) een willekeurige driehoek is met hoeken \(\alpha\), \(\beta\) en\(\gamma\) bij hoekpunten \(A\), \(B\) en \(C\), zijden van lengte \(a\), \(b\) en \(c\) tegenover \(A\), \(B\) en \(C\) zijn, en oppervlakte \(O\). In nevenstaande figuur is de situatie geschetst voor een driehoek met alleen scherpe hoeken.
We zullen voor deze situatie twee verbanden tussen de lengtes van de zijden en de hoeken bespreken en we zullen een oppervlakteformule bepalen, die overigens ook correct zijn als één van de hoeken van de driehoek stomp is.
sinusregel \[\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}\]
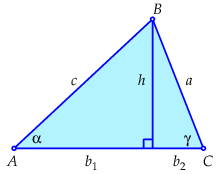
Stel dat de lengte van de hoogtelijn vanuit \(B\) naar de tegenoverliggende zijde \(AC\) gelijk is aan \(h\), zoals in nevenstaande figuur met alleen scherpe hoeken en \(b=b_1+b_2\). Dan geldt \(h=c\sin(\alpha)\) en \(h=a\sin(\gamma)\). Dus: \(c\sin(\alpha)=c\sin(\gamma)\), oftewel \(\frac{a}{\sin(\alpha)}=\frac{c}{\sin(\gamma)}\). De andere verbanden in de sinusregel kunnen op soortgelijke wijze aangetoond worden.
Voor de situatie met een stompe hoek, zeg \(\gamma\), kun je ook een hoogtelijn vanuit \(B\) tekenen maar ligt het punt op afstand \(h\) in het verlengde van het lijnstuk \(AC\). Dit vormt geen probleem voor het bewijs van de sinusregel als je bedenkt dat \(\sin(\pi-\gamma)=\sin(\gamma)\).
cosinusregel \[\begin{aligned} a^2 &= b^2+c^2-2bc\cos(\alpha)\\[0.25cm]
b^2 &= a^2+c^2-2ac\cos(\beta)\\[0.25cm] c^2 &= a^2+b^2-2ab\cos(\gamma)\end{aligned}\]
Stel de de lengte van de hoogtelijn vanuit \(B\) naar de tegenoverliggende zijde \(AC\) gelijk is aan \(h\), zoals in nevenstaande figuur met alleen scherpe hoeken en \(b=b_1+b_2\). Dan geldt volgens de stelling van Pythagoras \(c^2=b_1^2+h^2\) en \(a^2=b_2^2+ h^2\). Dus: \[\begin{aligned} c^2&=b_1^2+a^2-b_2^2\\[0.25cm] &= (b-b_2)^2+a^2-b_2^2\\[0.25cm] &=a^2+b^2-2b_2b\\[0.25cm] & a^2+b^2-2ab\cos(\gamma)\end{aligned}\] De andere versies van de cosinusregel worden op soortgelijke wijze aangetoond.
Voor de situatie met een stompe hoek, zeg \(\gamma\), kun je ook een hoogtelijn vanuit \(B\) tekenen maar ligt het punt op afstand \(h\) in het verlengde van het lijnstuk \(AC\). Dit vormt geen probleem voor het bewijs van de cosinusregel als je bedenkt dat \(\cos(\pi-\gamma)=-\cos(\gamma)\).
Oppervlakteformule \[O=\tfrac{1}{2}bc\sin(\alpha)=\tfrac{1}{2}ac\sin(\beta)=\tfrac{1}{2}ab\sin(\gamma)\]
Stel dat de lengte van de hoogtelijn vanuit \(B\) naar de tegenoverliggende zijde \(AC\) gelijk is aan \(h\), zoals in nevenstaande figuur met alleen scherpe hoeken. Dan geldt \(O=\tfrac{1}{2}bh\) en \(h=c\sin(\alpha)\). Dus: \(O=\tfrac{1}{2}bc\sin(\alpha)\). De andere verbanden voor de oppervlakte van de driehoek kunnen op soortgelijke wijze aangetoond worden.
Voor de situatie met een stompe hoek, zeg \(\gamma\), kun je ook een hoogtelijn vanuit \(B\) tekenen maar ligt het punt op afstand \(h\) in het verlengde van het lijnstuk \(AC\). Dit vormt geen probleem voor het bewijs van de oppervlakteregel als je bedenkt dat \(\sin(\pi-\gamma)=\sin(\gamma)\).
