Trigonometry: Inverse trigonometric functions
The arcsine, arccosine, and arctangent
When we know that \(\sin(x)=\tfrac{1}{2}\), then there are for \(x\) infinitely many possibilities. The sine is namely a periodic function, and in addition, each value between \(-1\) and \(1\) occurs twice during one period. Therefore, \(\sin(x)=\tfrac{1}{2}\) if \(x=\tfrac{1}{6}\pi\) and \(x=\tfrac{5}{6}\pi\), and we can add at any of those values an arbitrary multiple of \(2\pi\). However, all these options disappear once we agree that \(x\) is limited to the interval \([-\tfrac{1}{2}\pi, \tfrac{1}{2}\pi]\), that is, \(-\tfrac{1}{2}\pi\le x\le \tfrac{1}{2}\pi\). In this way we get the inverse trigonometric functions, which are also called cyclometric functions.
arcsin On the interval \([-\tfrac{1}{2}\pi, \tfrac{1}{2}\pi]\), the sine function is monotonously increasing and any function value is taken only once. Restricted to this interval there is therefore an inverse of the sine function, which we call the arcsine. We denote this function as \(x\mapsto\arcsin(x)\). Thus: \[\arcsin: [-1,1]\longrightarrow [-\tfrac{1}{2}\pi, \tfrac{1}{2}\pi]\] and the graph of arcsin looks as follows:
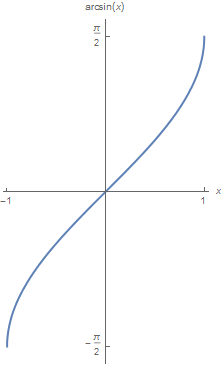The above graph originates from the graph of the sine function on the domain \([-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi]\) by reflection in the line \(y=x\).
arccos Consider the cosine function on the interval \([0,\pi]\), where the function is monotonically decreasing. Limited to this interval, there exists therefore an inverse, the arccosine. We denote this function as \(x \mapsto \arccos(x)\). Domain and range are as follows: \[\arccos: [-1,1] \longrightarrow [0,\pi]\] and the graph of arccos is as follows:
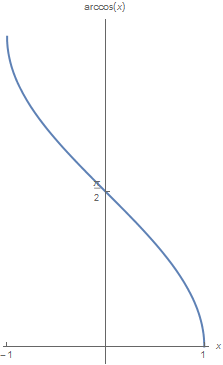
The above graph originates from the graph of the cosine function on the domain \([0,\pi]\) by reflection in the line \(y=x\).
arctan The tangent is function monotonously increasing on the interval \((-\tfrac{1}{2}\!\pi,\tfrac{1}{2}\pi)\). This interval is mapped into \(\mathbb{R}\). The inverse function, which maps the whole numberline \(\mathbb{R}\) onto the open interval \((-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi)\), is called the arctangent. We denote this function as \(x \mapsto \arctan(x)\) and its graph, obtained by reflecting the graph of the tangent on the interval \((-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi)\) in the line \(y=x\), is as follows:
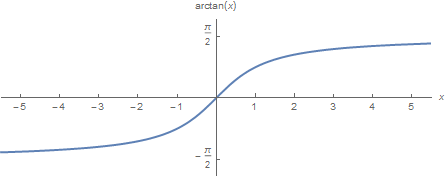
Note that the following applies: \[\lim_{x\to\infty}\arctan(x) = \frac{\pi}{2}\qquad\text{and}\qquad \lim_{x\to-\infty}\arctan(x) = -\frac{\pi}{2}\]
On the basis of the above definitions, the following statements are true:
\[\begin{aligned} x=\arcsin(y) &\iff y=\sin(x)\quad\text{and}\quad -\tfrac{1}{2}\pi\leq x\leq \tfrac{1}{2}\pi\\ x=\arccos(y) &\iff y=\cos(x)\quad\text{and}\qquad\quad 0\leq x\leq \pi\\ x=\arctan(y) &\iff y=\tan(x)\quad\text{and}\quad -\tfrac{1}{2}\!\pi\leq x\leq \tfrac{1}{2}\pi\end{aligned}\]
Written differently:
\[\begin{aligned} \arcsin\bigl(\sin(x)\bigr) = x & \quad \text{for }-\tfrac{1}{2}\pi\leq x\leq \tfrac{1}{2}\pi\\ \sin\bigl(\arcsin(x)\bigr) = x & \quad \text{for }\;\;\;-1\leq x\leq 1\\ \\ \arccos\bigl(\cos(x)\bigr) = x & \quad \text{for }\;\;\;\;0\leq x\leq \pi\\ \cos\bigl(\arccos(x)\bigr) = x & \quad \text{for }-1\leq x\leq 1\\ \\ \arctan\bigl(\tan(x)\bigr) = x & \quad \text{for }-\tfrac{1}{2}\pi\leq x\leq \tfrac{1}{2}\pi\\ \tan\bigl(\arctan(x)\bigr) = x & \quad \text{for all }x\end{aligned}\]
It are these characteristics that ensure that we speak loosely about inverse functions. It explains the following alternative notation for the inverse trigonometric functions, which you can come across in textbooks: \[\arcsin=\sin^{-1},\quad\arccos=\cos^{-1},\quad\arctan=\tan^{-1}\tiny.\] We avoid this notation as much as possible to prevent confusion with the functions \(\frac{1}{\sin x},\quad\frac{1}{\cos x}, \quad\frac{1}{\tan x}\). On a calculator, in programming languages, and in textbooks you can also come across the names \(\mathrm{asin}\), \(\mathrm{acos}\), and \(\mathrm{ atan}\) for the inverse trigonometric functions.
The naming convention starting with \(\mathrm{arc}\) indicates that \(\mathrm{\arccos}\) and \(\mathrm{\arcsin}\) have to do with the length of a circular arc: \(\arccos(x\) is the length of the arc on the unit circle that starts at the point \((1,0)\) and goes to the point with horizontal coordinate \(x\) \(\arcsin(y)\) is the directed length of the arc on the unit circle that starts at the point \((1,0)\) and goes to the point with vertical coordinate \(y\).
\(\phantom{x}\)
Another property of arccosine and arcsine is:
If \(-1\le x\le 1\), then \(\arccos(x)=\tfrac{1}{2}\pi-\arcsin(x)\) .
