De arcsinus, arccosinus en arctangens

Goniometrische functies en hun inversen: Inverse goniometrische functies

De arcsinus, arccosinus en arctangens

Wanneer we weten dat $\sin(x)=\tfrac{1}{2}$ , dan zijn er voor $x$ nog oneindig veel mogelijkheden open. De sinus is namelijk een periodieke functie, en bovendien wordt elke waarde tussen $-1$ en $1$ gedurende één periode tweemaal aangenomen. Zo geldt $\sin(x)=\tfrac{1}{2}$ als $x=\tfrac{1}{6}\pi$ en $x=\tfrac{5}{6}\pi$ en bij elke van die waarden kunnen we nog een willekeurig veelvoud van $2\pi$ optellen. Al die keuzemogelijkheden verdwijnen echter wanneer we afspreken dat we $x$ beperken tot het interval $[-\tfrac{1}{2}\pi, \tfrac{1}{2}\pi]$ , dat wil zeggen voor $-\tfrac{1}{2}\pi\le x\le \tfrac{1}{2}\pi$ . Zo ontstaan de inverse goniometrische functies, die ook wel cyclometrische functies genoemd worden.

Op het interval $[-\tfrac{1}{2}\pi, \tfrac{1}{2}\pi]$ is de sinusfunctie monotoon stijgend en wordt elke functiewaarde maar eenmaal aangenomen. Beperkt tot dit interval bestaat er daarom een inverse van de sinusfunctie en die noemen we de arcsinus. We noteren deze functie als $x\mapsto\arcsin(x)$ . Er geldt: $\arcsin: [-1,1]\longrightarrow [-\tfrac{1}{2}\pi, \tfrac{1}{2}\pi]$ en de grafiek van arcsin ziet er als volgt uit:

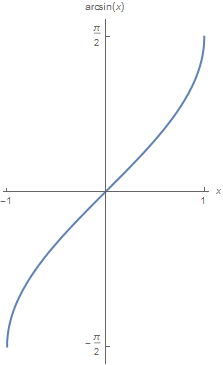grafiek van arcssin Bovenstaande grafiek ontstaat uit de grafiek van de sinusfunctie op het domein $[-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi]$ door spiegeling in de lijn $y=x$ .

Beschouw de cosinusfunctie op het interval $[0,\pi]$ , waar de functie monotoon dalend is. Beperkt tot dit interval bestaat er daarom een inverse, de arccosinus. We noteren deze functie als $x \mapsto \arccos(x)$ . Domein en bereik zijn als volgt: $\arccos: [-1,1] \longrightarrow [0,\pi]$ en de grafiek van arccos ziet er als volgt uit:

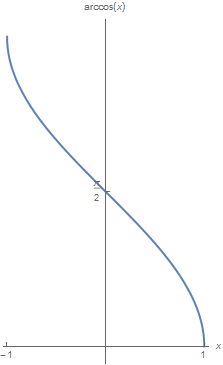
grafiek van arccos

Bovenstaande grafiek ontstaat uit de grafiek van de cosinusfunctie op het domein $[0,\pi]$ door spiegeling in de lijn $y=x$ .

De tangens is monotoon op het interval $(-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi)$ . Dit interval wordt afgebeeld op ${\mathbb R}$ . De inverse functie, die dus de hele lijn $\mathbb{R}$ afbeeldt op het begrensde open interval $(-\tfrac{1}{2}\!\pi,\tfrac{1}{2}\pi)$ , heet de arctangens. We noteren deze functie als $x \mapsto \arctan(x)$ en de grafiek, verkregen door spiegeling van de grafiek van de tangens op het interval $(-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi)$ in de lijn $y=x$ , ziet er als volgt uit:

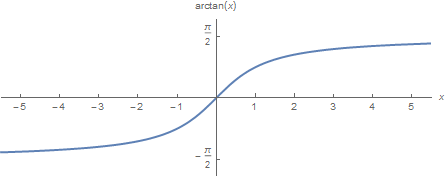
grafiek van arctan

Merk op dat geldt: $\lim_{x\to\infty}\arctan(x) = \frac{\pi}{2}\qquad\text{en}\qquad \lim_{x\to-\infty}\arctan(x) = -\frac{\pi}{2}$

Op basis van bovenstaande definities geldt:

$\begin{aligned} x=\arcsin(y) &\iff y=\sin(x)\quad\text{en}\quad -\tfrac{1}{2}\pi\leq x\leq \tfrac{1}{2}\pi\\ x=\arccos(y) &\iff y=\cos(x)\quad\text{en}\qquad\quad 0\leq x\leq \pi\\ x=\arctan(y) &\iff y=\tan(x)\quad\text{en}\quad -\tfrac{1}{2}\!\pi\leq x\leq \tfrac{1}{2}\pi\end{aligned}$

Iets anders opgeschreven luidt de regel:

$\begin{aligned} \arcsin\bigl(\sin(x)\bigr) = x & \quad \text{voor }-\tfrac{1}{2}\pi\leq x\leq \tfrac{1}{2}\pi\\ \sin\bigl(\arcsin(x)\bigr) = x & \quad \text{voor }\;\;\;-1\leq x\leq 1\\ \\ \arccos\bigl(\cos(x)\bigr) = x & \quad \text{voor }\;\;\;\;0\leq x\leq \pi\\ \cos\bigl(\arccos(x)\bigr) = x & \quad \text{voor }-1\leq x\leq 1\\ \\ \arctan\bigl(\tan(x)\bigr) = x & \quad \text{voor }-\tfrac{1}{2}\pi\leq x\leq \tfrac{1}{2}\pi\\ \tan\bigl(\arctan(x)\bigr) = x & \quad \text{voor alle }x\end{aligned}$

Het zijn deze eigenschappen dat er voor zorgen dat we losjes spreken over inverse functies. Het verklaart de volgende alternatieve notatie voor de inverse goniometrische functies, die je in handboeken tegen kunt komen: $\arcsin=\sin^{-1},\quad\arccos=\cos^{-1},\quad\arctan=\tan^{-1}\tiny.$ We vermijden deze notatie zo veel mogelijk om verwarring met de functies $\frac{1}{\sin x},\quad\frac{1}{\cos x}, \quad\frac{1}{\tan x}$ te voorkomen. Op rekenmachines, in programmeertalen en in handboeken kun je ook nog de namen $\mathrm{asin}$ , $\mathrm{acos}$ en $\mathrm{ atan}$ tegenkomen voor de inverse goniometrische functies.

De naamgeving beginnend met $\mathrm{arc}$ geeft aan dat $\mathrm{\arccos}$ en $\mathrm{\arcsin}$ te maken hebben met de lengte van een cirkelboog (arc = boog in de Engelse taal): $\arccos(x)$ is de lengte van de cirkelboog op de eenheidscirkel de begint op het punt $(1,0)$ en gaat tot het punt met horizontale coördinaat $x$ . $\arcsin(y)$ is de gerichte lengte van de cirkelboog op de eenheidscirkel de begint op het punt $(1,0)$ en gaat tot het punt met verticale coördinaaat $y$ .

$\phantom{x}$

Nog een eigenschap van arccosinus en arcsinus is:

Als $-1\le x\le 1$ , dan $\arccos(x)=\tfrac{1}{2}\pi-\arcsin(x)$ .

Voor de liefhebber geven we een bewijs van de bewering dat $\arccos(x)=\tfrac{1}{2}\pi-\arcsin(x)$ als $-1\le x\le 1$ . Voor alle waarden van $y$ geldt $\cos(\tfrac{1}{2}\pi-y)=\sin(y)\tiny.$ Neem $y=\arcsin(x)$ met $-1\le x\le 1$ , dan krijg je na vereenvoudiging $\cos\bigl(\tfrac{1}{2}\pi-\arcsin(x)\bigr)=x\tiny.$ Pas aan weerszijden de arccosinus toe en vereenvoudig: $\tfrac{1}{2}\pi-\arcsin(x)=\arccos(x)\tiny.$