Trigonometry: Trigonometric functions
Trigonometry in right-angled triangles
Probably the first time that you came across the sine, cosine and tangent is as length ratio of sides of a right-angled triangle. We recap the definitions.
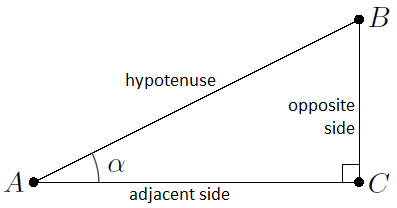
Vertices of triangles we label with capitals as \(A\), \(B\), \(C\). The length of the side \(BC\), the line segment between \(B\) and \(C\) opposite of point \(A\), is denoted by \(|BC|\) or by the lowercase character \(a\). The size of the angles, we indicate with Greek letters such as, for example, \(\alpha\) for the angle in \(A\). we measure angles in general in degrees, but also the use of the radians is allowed. See the figure below of a right-angled triangle (the angle in \(C\) is \(90^\circ\) and this is denoted by the special symbol of a small square near the vertex \(C\)).
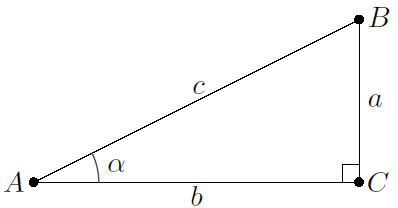
If \(A\), \(B\) and \(C\) are the vertices of a right-angled triangle as shown above, then we define for the angle \(\alpha\) in \(A\): \[\begin{aligned}\sin(\alpha)&= \dfrac{|BC|}{|AB|}=\dfrac{a}{c}, \qquad\cos(\alpha) = \dfrac{|AC|}{|AB|}=\dfrac{b}{c}, \\ \\
\tan(\alpha)&= \dfrac{\sin(\alpha)}{\cos(\alpha)}=\dfrac{|BC|}{|AC|}=\dfrac{a}{b}\end{aligned}\]
Pythagorean theorem The area of the square whose side is the hypotenuse (the side opposite of the vertex with the right angle) is equal to the sum of the areas of the squares on the other two sides in a right-angled triange. In the right-angled triangle shown above, the length of the sides are therefore related as follows: \[a^2+b^2=c^2\]
Mnemonic A mnemonic to recall the definitions of sine, cosine en tangent in right-angled triangles is the SOHCAHTOA acronym:
- SOH = Sine of the angle is the length of the Opposite side divided by the length of the Hypotenuse, which is the slanted long side of the right-angled triangle;
- CAH = Cosine of the angle is the length of the Adjacent side divided by the length of the Hypotenuse;
- TOA = Tangent of the angle is the length of the Opposite side divided by the length of the Adjacent side.
The meaning of the opposite, adjacent and slanted side (hypotenuse) of a right-angled triangle is show in the figure below
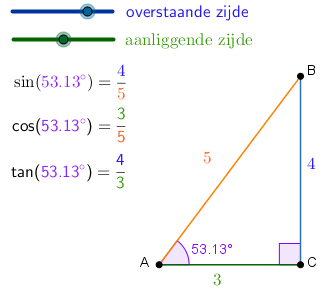
Interactive example By dragging the sliders in the interactive diagram below you can construct other right-angled triangles and explore how trigonometric values are determined.
Consider a right-angled triangle \(ABC\) with an angle \(\alpha\) in vertex \(A\) and a right angle in vertex \(C\) as indicated in the figure below. Given are the lengths \(c = 10\) and \(b=6\).
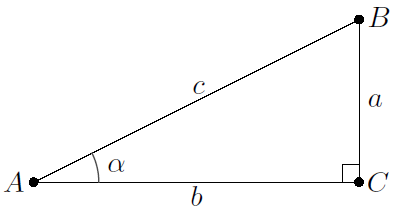
To see this, we use \(\sin(\alpha) = \dfrac{a}{c}= \dfrac{a}{10}\). We calculate the length of \(BC\) via the Pythagorean theorem, which in our notation is equivalent to : \[a^2+b^2=c^2\] So: \[\begin{aligned}a^2 &= c^2-b^2\\[0.25cm] &= {10}^2-{6}^2\\[0.25cm] &= (10-6)\times(10+6)\\[0.25cm] &=4\times16\\[0.25cm] &=64\\[0.25cm] &= 8^2\end{aligned}\] Thus: \(a = 8\). We conclude that \(\displaystyle\sin(\alpha) =\frac{8}{10}= {{4}\over{5}}\).
