Goniometrische functies en hun inversen: Goniometrische functies
Goniometrie bij rechthoekige driehoeken
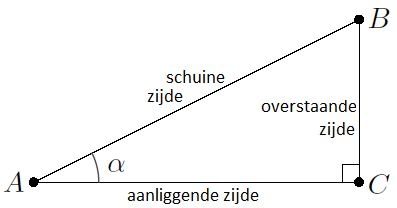
De sinus, cosinus en tangens kom je voor het eerst tegen als lengteverhoudingen tussen zijden van een rechthoekige driehoek. We recapituleren de definities.
De hoekpunten van driehoeken geven we met hoofdletters aan (als \(A\), \(B\), \(C\). De lengte van de zijde \(BC\), het lijnstuk tussen \(B\) en \(C\) tegenover het punt \(A\), geven we aan met \(|BC|\) of met de kleine letter \(a\). De grootte van de hoeken geven we aan met Griekse letters, zoals bijvoorbeeld \(\alpha\) voor de hoek in A. We meten hoeken in het algemeen in graden, maar ook het gebruik van radialen is mogelijk. Zie onderstaande figuur van een rechthoekige driehoek (de hoek in \(C\) is \(90^\circ\)).
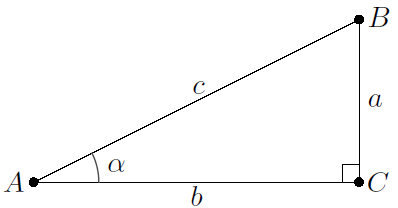
Als \(A\), \(B\) en \(C\) de hoekpunten zijn van een rechthoekige driehoek zoals hierboven getekend, dan geldt voor de hoek \(\alpha\) in \(A\):
\[\begin{aligned}\sin(\alpha)&= \dfrac{|BC|}{|AB|}=\dfrac{a}{c}, \qquad\cos(\alpha) = \dfrac{|AC|}{|AB|}=\dfrac{b}{c}, \\ \\
\tan(\alpha)&= \dfrac{\sin(\alpha)}{\cos(\alpha)}=\dfrac{|BC|}{|AC|}=\dfrac{a}{b}\end{aligned}\]
Stelling van Pythagoras In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde. In bovenstaande rechthoekige driehoek zijn de lengten van de zijden dus als volgt gerelateerd: \[a^2+b^2=c^2\]
Ezelsbruggetje Een ezelsbruggetje voor het onthouden van de definities van de sinus, cosinus en tangens in rechthoekige driehoeken is het SOSCASTOA acroniem:
- SOS = Sinus van de hoek is de lengte van de Overstaande zijde gedeeld door de lengte van de Schuine zijde;
- CAS = Cosinus van de hoek is de lengte van de Aanliggende zijde gedeeld door de lengte van de Schuine zijde;
- TOA = Tangens van de hoek is de lengte van de Overstaande zijde gedeeld door de lengte van de Aanliggende zijde.
Hierbij is de betekenis van de overstaande, aanliggende en schuine zijde van een rechthoekige driehoek als in onderstaande figuur.
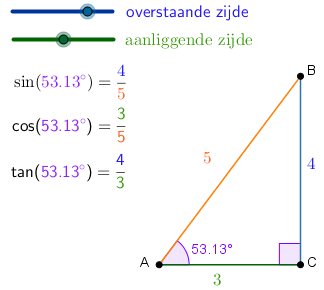
Interactief voorbeeld Met de schuifbalken kun je andere rechthoekige driehoeken maken en zien hoe goniometrische waarden bepaald worden.
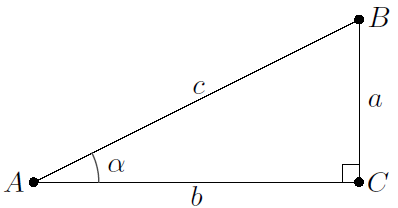
Om dit in te zien, gebruiken we \(\sin(\alpha) = \dfrac{a}{c}= \dfrac{a}{50}\). De lengte van \(BC\) berekenen we met de stelling van Pythagoras, die met onze letterkeuze gelijk is aan: \[a^2+b^2=c^2\tiny.\] Dus: \[\begin{aligned}a^2 &= c^2-b^2\\[0.25cm] &= {50}^2-{14}^2\\[0.25cm] &= (50-14)\times(50+14)\\[0.25cm] &=36\times64\\[0.25cm] &=2304\\[0.25cm] &= 48^2\end{aligned}\] Dus \(a = 48\). We concluderen dat \(\displaystyle\sin(\alpha) =\frac{48}{50}= {{24}\over{25}}\).
