Trigonometry: Trigonometric functions
 Definitions of trigonometric functions
Definitions of trigonometric functions
You came across the sine, cosine and tangent as length ratios of sides of a right-angled triangle. But now we consider the related sine function sin, cosine function cos, and tangent function tan, that is, functions defined for real numbers and not just for acute angles in a rectangular triangle. For the definition of the trigonometric functions sin, cos and tan it is convenient to the unit circle \(C\), which is the circle the origin as centre and with radius 1.
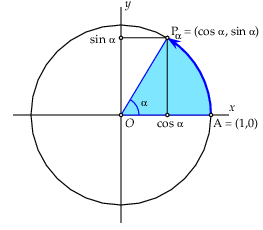
sin and cos Let \(A\) be the point \((1,0)\) on the unit circle \(C\) and define for any positive number \(\alpha\) the point \(P_{\alpha}\) on \(C\) as the point obtained by moving \(A\) anticlockwise along the rim of the unit circle over a distance \(\alpha\). The point \(P_{\alpha}\) has then by definition the coordinates \(\bigl(\cos(\alpha), \sin(\alpha)\bigr)\); for readability, we often omit some brackets and write \(\bigl(\cos\alpha, \sin\alpha\bigr)\). The figure below visualizes this definition. For any negative number \(\alpha\) a similar definition applies, but then the movement of the point \(A\) must be in the clockwise direction.
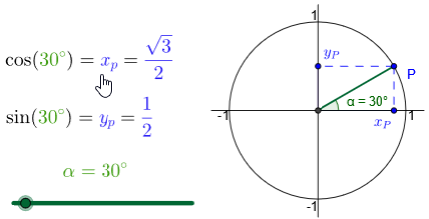
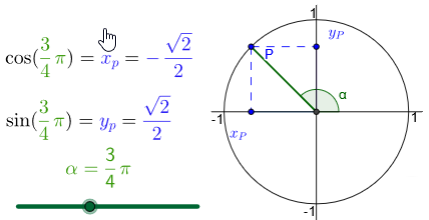
Special function values The interactive figures below show cosine ansd sine values for special rotation angels in degrees and radians.
\(\phantom{abc}\)
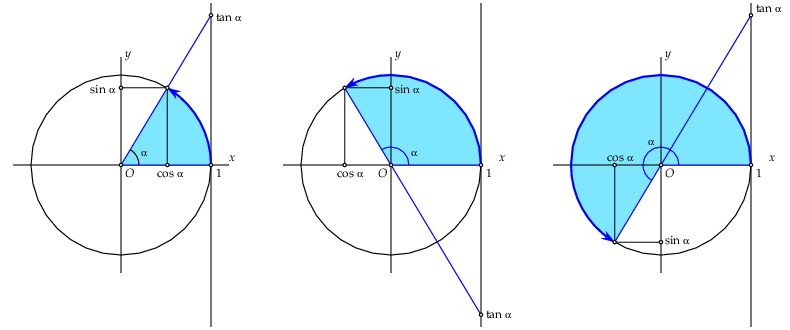
tan The tangent function can be defined as the quotient of the sine and cosine function, but can also be visualized using the unit circle. Draw a vertical line through the point \((1,0)\) and intersect the extended radius with that line. The \(y\)-coordinate of the intersection point is then \((1,\tan\alpha)\). Several cases for different values of \(\alpha\) are shown in the figures below.
Mathcentre video
Trigonometric Ratios of Any Angle (28:40)