Goniometrische functies en hun inversen: Goniometrische functies
 Definities van goniometrische functies
Definities van goniometrische functies
De sinus, cosinus en tangens ben je tegengekomen als lengteverhoudingen tussen zijden van een rechthoekige driehoek. Maar nu bekijken we de hiermee gerelateerde sinusfunctie sin, cosinusfunctie cos, en tangensfunctie tan, d.w.z. functies gedefinieerd voor reële getallen en niet alleen voor scherpe hoeken in een rechthoekige driehoek. Voor de definitie van de goniometrische functies sin, cos en tan is het handig om de eenheidscirkel \(C\), zijnde de cirkel met straal 1 en de oorsprong O als middelpunt, te gebruiken.
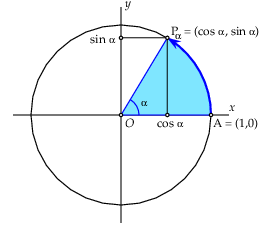
sin en cos Laat \(A\) het punt \((1,0)\) op de eenheidscirkel \(C\) zijn en definieer voor elk positief getal \(\alpha\) het punt \(P_{\alpha}\) op \(C\) als het punt verkregen door \(A\) te verplaatsen langs de rand van de eenheidscirkel tegen de wijzers van de klok in over een afstand \(\alpha\). Het punt \(P_{\alpha}\) heeft dan per definitie de coördinaten \(\bigl(\cos(\alpha), \sin(\alpha)\bigr)\); voor de leesbaarheid laten we vaak wat haakjes weg en schrijven dan \(\bigl(\cos\alpha, \sin\alpha\bigr)\). Onderstaande figuur visualiseert deze definitie. Voor elk negatief getal \(\alpha\) kan eenzelfde definitie gemaakt worden met dien verstande dat de verplaatsing van het punt \(A\) dan met de wijzers van de klok mee is.
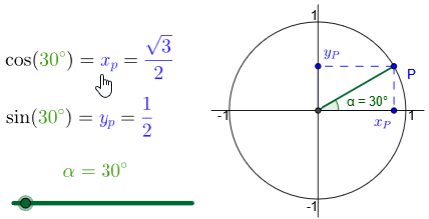
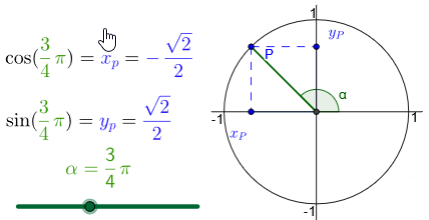
Speciale functiewaarden Onderstaande interactieve figuren tonen de cosinus- en sinuswaarden voor speciale draaiingshoeken in graden en radialen.
\(\phantom{abc}\)
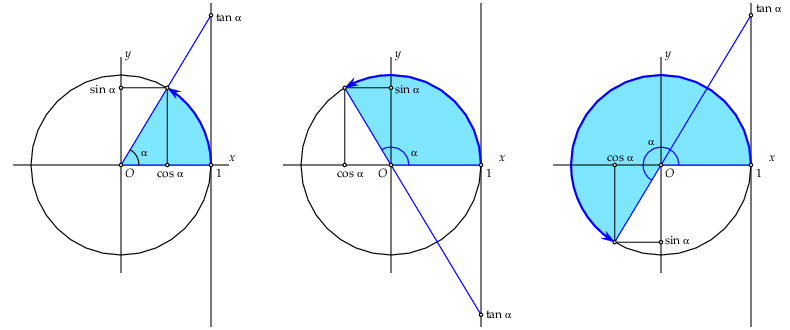
tan De tangensfunctie kan gedefinieerd worden als het quotiënt van de sinus- en cosinusfunctie, maar is ook m.b.v. de eenheidscirkel te visualiseren. Teken de verticale lijn door het punt \((1,0)\) en snijd de verlengde straal met die lijn. De \(y\)-coördinaat van het snijpunt is dan \((1,\tan\alpha)\). In onderstaande figuur is de situatie voor verschillende waarden van \(\alpha\) getekend.
Mathcentre video
Trigonometric Ratios of Any Angle (28:40)