Goniometrische functies en hun inversen: Goniometrische functies
Grafieken van goniometrische functies
Hieronder zijn de grafieken getekend van de functies \(\sin(x)\), \(\cos(x)\) en \(\tan(x)\).
Deze functies zijn periodiek: voor de sinus- en cosinusfunctie is de periode gelijk \(2\pi\) en
voor de tangensfunctie is de periode gelijk aan \(\pi\). De sinus- en cosinusgrafieken schommelen om de evenwichtsstand \(0\) en de maximale uitwijking, ook wel amplitude genaamd, is gelijk aan \(1\).
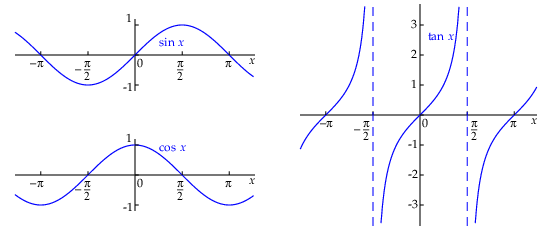
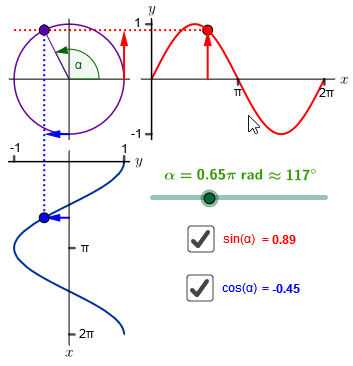
Interactieve visualisatie van de sinus en cosinusgrafiek Onderstaande interactieve visualisatie is bedoeld om meer inzicht in de grafiek van de sinus- en cosinusfunctie te krijgen. De sinusgrafiek is in de gebruikelijke oriëntatie (positieve \(x\)-as naar rechts en positieve \(y\)-as naar boven) getekend; de cosinusgrafiek is een kwartslag gedraaid (positieve \(x\)-as is naar beneden en positieve \(y\)-as naar rechts).
Klik op de animatieknop linksonder om een animatie te starten en te stoppen. Je kunt ook met de muis de schuifbalk bewegen en de functies selecteren.
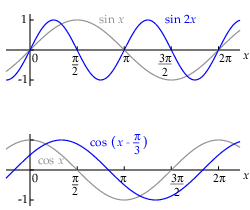
Transformaties Hieronder staan voorbeelden getekend van twee veelgebruikte transformaties. In de bovenste van de twee figuren vind je behalve de grafiek van de functie \(\sin(x)\) ook die van \(\sin(2x)\). De sinusgrafiek is in horizontale richting als het ware met een factor 2 samengedrukt. De periode is tweemaal zo klein geworden: \(\pi\) i.p.v. \(2\pi\).
De onderste tekening toont naast de grafiek van \(\cos(x)\) ook die van de functie \(\cos(x - \frac{\pi}{3})\). De cosinusgrafiek is nu in horizontale richting over een afstand van \(\frac{\pi}{3}\) naar rechts verschoven.
We behandelen transformaties van de sinusfunctie en zijn grafiek nog op een meer systematische wijze.
