Trigonometry: Trigonometric functions
 Signals in the time domain
Signals in the time domain
From now on we use the independent variable \(t\) because we usually will interpret it as time. A function \(s(t)\) of \(t\) is then called a (time) signal.
A signal of the form \[s(t)=A \sin(2\pi f t+\varphi)\] is called an alternating signal (also known as sinusoid) with amplitude \(A\), frequency \(f\) and phase \(\varphi\).
We will always assume that \(A\) and \(f\) are positive numbers and call this formula the standard form.
The amplitude determines the size of the oscillations.
The frequency determines the number of oscillations in the time interval [0,1].
The unit of frequency, that is, the number of periods per second, is hertz (Hz).
The phase is related to a horizontal translation
(to the left for positive \(\varphi\), to the right for negative \(\varphi\)).
The number \(\displaystyle T=\frac{1}{f}\) is the period of the alternating signal, because \(T\) is the smallest positive integer with the property that \[s(t+T)=s(t)\] for all \(t\).
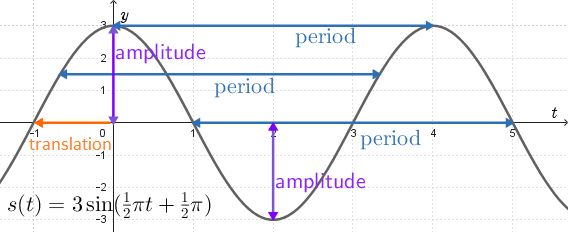
In the figure to the right we have draen the graph of the sinusod defined by \(s(t)=3\sin\left(\tfrac{1}{2}\pi+\tfrac{1}{2}\pi\right)\). We denote herein the amplitude (\(3\)), the period (\(4\)) en and the horizontal translation (\(-1\)) of a sine graph that has, in this exampe, a phase of \(\tfrac{1}{2}\pi\).
Alternating signal as a sum of sine and cosine By making use of the addition formulas any alternating signal can also be written in the form \[s(t)=a \sin(2\pi f t)+b \cos(2\pi f t)\] Here\[a=A\cos(\varphi)\quad\text{and}\quad b=A\sin(\varphi)\]
Conversely, any signal of the form \[s(t)=a \sin(2\pi f t)+b \cos(2\pi f t)\] can be written in standard form. You must determine \(A\) and \(\varphi\) so that at least \[A=\sqrt{a^2+b^2}\quad\text{and}\quad \tan(\varphi)=\frac{\sin(\varphi)}{\cos(\varphi)}=\frac{b}{a}\] The appropriate phase \(\varphi\) is fixed modulo \(2\pi\).


