Goniometrische functies en hun inversen: Goniometrische functies
 Signalen in het tijddomein
Signalen in het tijddomein
Vanaf nu gebruiken we de onafhankelijke variabele \(t\), omdat we die meestal zullen interpreteren als de tijd. Een functie \(s(t)\) van \(t\) heet dan een (tijd)signaal.
Een signaal van de vorm \[s(t)=A \sin(2\pi f t+\varphi)\] heet een wisselsignaal (of ook wel sinusoïde) met amplitude \(A\), frequentie \(f\) en fase \(\varphi\).
We zullen altijd aannemen dat \(A\) en \(f\) positieve getallen zijn en noemen deze formule de zogenaamde standaardvorm.
De amplitude bepaalt de grootte van de oscillaties.
De frequentie bepaalt het aantal oscillaties op het tijdsinterval [0,1].
De eenheid van frequentie, d.w.z. het aantal perioden per seconde, is hertz (Hz).
De fase houdt verband met een horizontale verplaatsing
(naar links bij positieve \(\varphi\); naar rechts bij negatieve \(\varphi\)).
Het getal \(\displaystyle T=\frac{1}{f}\) is de periode van het wisselsignaal, want \(T\) is het kleinste positieve getal met de eigenschap dat \[s(t+T)=s(t)\] voor alle \(t\).
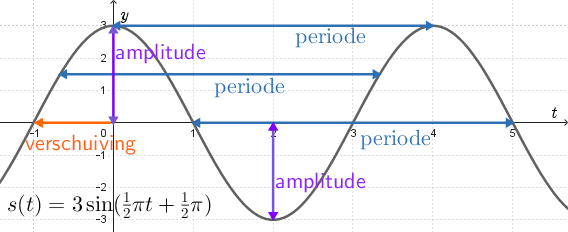
In nevenstaande figuur is de grafiek getekend van de sinusoïde gedefinieerd als \(s(t)=3\sin\left(\tfrac{1}{2}\pi+\tfrac{1}{2}\pi\right)\). Hierin zijn aangegeven de amplitude (\(3\)), de periode (\(4\)) en de horizontale verschuiving (\(-1\)) van een sinusgrafiek die in dit voorbeeld bij de fase van \(\tfrac{1}{2}\pi\) past.
Wisselsignaal als som van sinus en cosinus Door gebruik te maken van de optelformules kan elk wisselsignaal ook in de vorm \[s(t)=a \sin(2\pi f t)+b \cos(2\pi f t)\] geschreven worden. Daarbij is \[a=A \cos(\varphi)\quad\text{en}\quad b=A \sin(\varphi)\]
Omgekeerd kan elk signaal van de vorm \[s(t)=a \sin(2\pi f t)+b \cos(2\pi f t)\] in de standaardvorm genoteerd worden. Je moet \(A\) en \(\varphi\) dan zo bepalen dat in ieder geval \[A=\sqrt{a^2+b^2}\quad\text{en}\quad \tan(\varphi)=\frac{\sin(\varphi)}{\cos(\varphi)}=\frac{b}{a}\] De geschikte fase \(\varphi\) ligt op veelvouden van \(2\pi\) na vast.


