Goniometrische functies en hun inversen: Goniometrische functies
 Willekeurige periodieke signalen
Willekeurige periodieke signalen
Een willekeurig signaal \(s(t)\) heet periodiek met periode \(T\) (ook wel trillingstijd genoemd) als \(T\) het kleinste positieve getal is met de eigenschap dat \[s(t+T)=s(t)\] voor alle \(t\).
Bij zo'n signaal is de frequentie \(f\) weer gedefinieerd als \[f=\frac{1}{T}\] Het getal \(f\) is het aantal perioden ('trillingen') per tijdseenheid.
Als regel is \(f\) dus het aantal trillingen per seconde; men meet de frequentie dan in hertz (Hz).
Onder de evenwichtsstand van zo'n signaal verstaat men de gemiddelde waarde over één periode.
De amplitude van \(s(t)\) is de maximale afwijking van de evenwichtsstand.
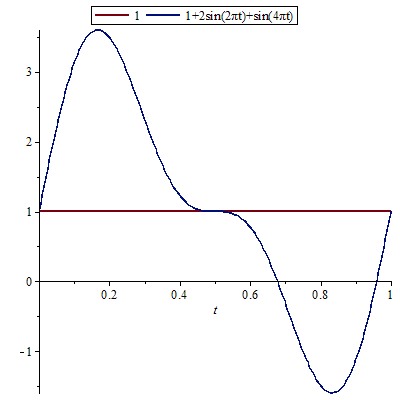
De grafiek van het signaal \[s(t)=1+2\sin(2\pi t)+\sin(4\pi t)\] is hieronder getekend, samen met de evenwichtsstand die gelijk is aan 1.
De amplitude is exact te berekenen: de functie neemt op het getoonde tijdsinterval de maximale waarde aan voor \(t=\tfrac{1}{6}\) en deze waarde is gelijk aan \(1+\tfrac{3}{2}\!\sqrt{3}\). De amplitude van het signaal is dus gelijk aan \(\tfrac{3}{2}\!\sqrt{3}\approx 2.6\).
Bovenstaand voorbeeld mag gekunsteld lijken, maar kom je in praktijk wel tegen. We geven twee voorbeelden, het ene uit biomechanica en het andere uit getijdenanalyse.
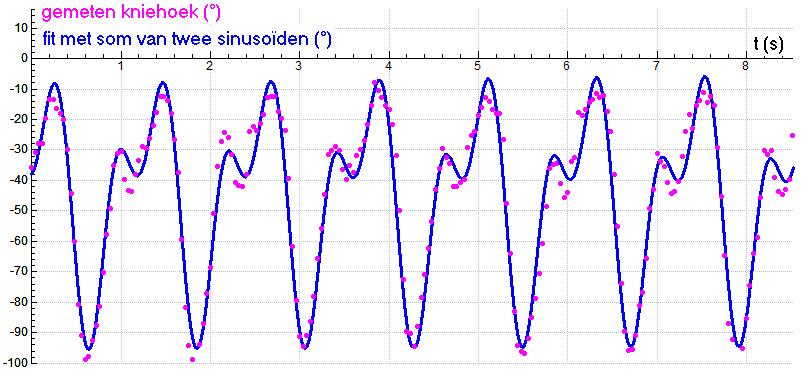
Dit voorbeeld komt uit de biomechanica en gaat over de kniehoek (in graden) tijdens huppelen.
Metingen op videobeelden van de beweging zijn in onderstaande figuur in grafiekvorm uitgezet samen met de grafiek van een benadering met behulp van twee sinusoïden en een constante. De wiskundige formule van deze benadering is \[\mathrm{kniehoek\;}({}^{\circ})=-45.0+31.0\cdot\sin(2\pi\cdot 0.82\cdot t+1.11)+21.1\cdot\sin(2\pi\cdot1.65\cdot t-1.74)\] Bij benadering is de frequentie van het signaal dus gelijk aan \(0.82\) Hz. Bij benadering is de evenwichtsstand gelijk aan \(-45^{\circ}\) en de amplitude gelijk aan \(50^{\circ}\). Deze twee waarden zijn overigens niet in de grafiek af te lezen, maar moeten numeriek bepaald worden over een periode.
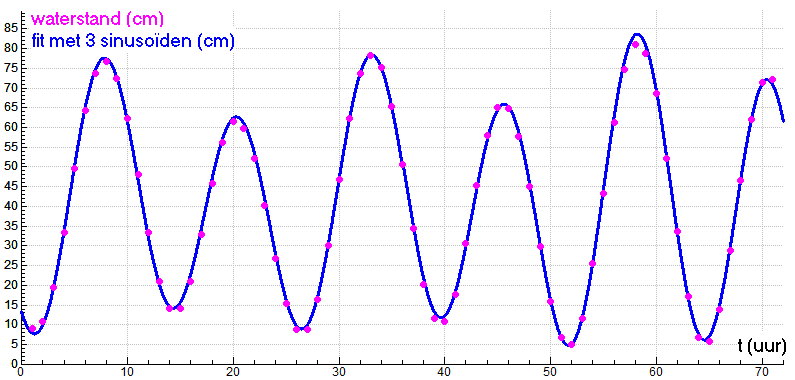
Dit is een voorbeeld van een analyse van het getij. We hebben hier gekozen voor de analyse van het getij in Sewells Point (Virginia, USA) van 23 maart t/m 25 maart 2006. Metingen zijn in onderstaande figuur in grafiekvorm uitgezet samen met de grafiek van een benadering met behulp van drie sinusoïden en een constante. De wiskundige formule van deze benadering is \begin{eqnarray*}\mathrm{waterstand\;(cm)} &=& 40.9+31.0\cdot\sin(0.506\cdot t-2.463) \\ & & +8.8\cdot\sin(0.535\cdot t+0.165)+7.7\sin(0.251\cdot t=0.745)\end{eqnarray*}