Goniometrische functies en hun inversen: Goniometrische functies
 Signaalanalyse
Signaalanalyse
Signaalanalyse (ook wel harmonische analyse genoemd) is gebaseerd op de eigenschap dat elk periodiek signaal \(s(t)\) met periode \(T\), en dus met frequentie \(f=T^{-1}\), geschreven kan worden als mogelijk oneindige som van sinusoïden met frequenties die een veelvoud van \(f\) zijn, mits het signaal maar een voldoende nette functie is. We laten in het midden wat de zogenaamde Dirichlet condities voor netheid van de functie precies zijn, maar alle praktische signalen voldoen aan deze condities. We kunnen dus het volgende opschrijven voor een periodiek signaal \(s(t)\):
\[\begin{aligned} s(t) &= c + \sum_{n=1}^{\infty} c_n\cdot\sin(2\pi\cdot n\cdot f\cdot t+\phi_n)\\ \\
&= c + \sum_{n=1}^{\infty} a_n\cdot\cos(2\pi\cdot n\cdot f\cdot t)+\sum_{n=1}^{\infty} b_n\cdot\sin(2\pi\cdot n\cdot f\cdot t)
\end{aligned}\]
De grootte van de coëfficiënten \(c\), \(a_n\), \(b_n\) en \(c_n\) in deze zogenaamde Fourierreeks kunnen via Fourier integralen berekend worden, maar we gaan hier niet verder op in. We volstaan met de opmerking dat de rij \(c_1, c_2, c_3, \ldots\) het amplitudespectrum genoemd wordt en dat de rij \(\phi_1, \phi_2, \phi_3, \ldots\) het fasespectrum heet. De staafgrafiek van de functie \(n\mapsto c_n\) heet het frequentie-amplitudespectrum van het signaal \(s(t)\). De staafgrafiek van de functie \(n\mapsto c_n^2\) heet het vermogensspectrum van het signaal \(s(t)\); vaak wordt deze genormaliseerd door het totale vermogen \(\displaystyle \sum_{n=1}^{\infty}c_n^2\).
De eerste term \(c_1\sin(2\pi f t+\phi_1)\) in het signaal heet de grondharmonische, de tweede term \(c_2\sin(4\pi f t+\phi_2)\) heet de tweede harmonische of eerste boventoon, enzovoort. Als het signaal een geluidssignaal is spreekt men van een grondtoon met frequentie \(f\) en boventonen met frequenties \(n\cdot f\) voor \(n=2,3,\cdots\).
Het eerdere voorbeeld van de kniehoek tijdens huppelen is een eenvoudig voorbeeld van een eindige Fourier reeeks, in dit geval met slechts twee sinusoïden. We behandelen nog twee voorbeelden.
We bekijken het bloksignaal \(s(t)\) gedefinieerd als de periodieke voortzetting van de functie \[\sigma(t)=\begin{cases} -1 & \text{als \(-\pi\le t<0\)}\\ 1 & \text{als \(0< t\le \pi\)}\end{cases}\]
De Fourier reeks van dit signaal is als volgt: \[\begin{aligned} s(t) &= \frac{4}{\pi}\sin(t)+\frac{4}{3\pi}\sin(3t) +\frac{4}{5\pi}\sin(5t)+\frac{4}{7\pi}\sin(7t)+\cdots\\ \\
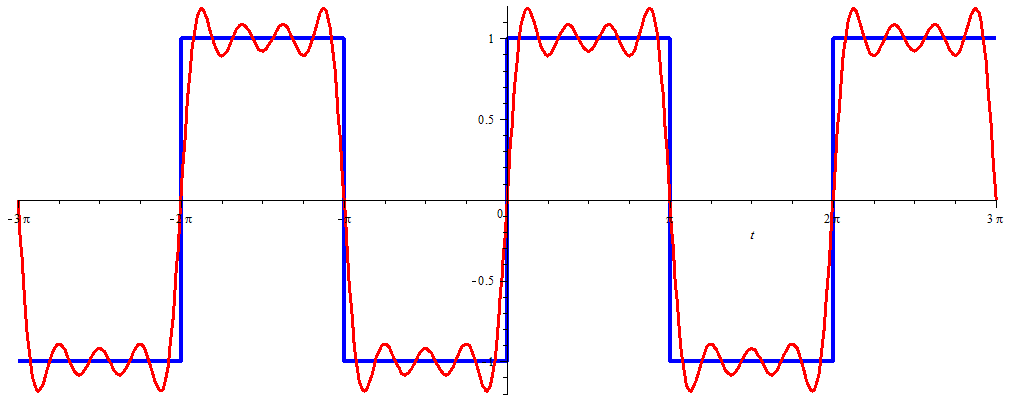
&=\frac{4}{\pi}\sum_{n=1}^{\infty} \frac{\sin\bigl((2n-1)t\bigr)}{2n-1}\end{aligned}\] Onderstaande grafiek toont het bloksignaal en de grafiek van de som van de eerste vier termen in de Fourierreeks.
Dit voorbeeld komt uit muziektheorie. Twee tonen die gelijktijdig klinken vormen een interval. Hebben de frequenties van die tonen een eenvoudige trillingsgetalverhouding, dan klinkt de samenklank harmonieus. In de muziektheorie zijn er traditionele namen in gebruik, bijvoorbeeld een octaaf voor de trillingsgetalverhouding 1:2 en grote terts voor de trillingsgetalverhouding 4:5.
Laten we eens bekijken wat voor signaal er ontstaat als wanneer we twee zuivere sinustonen samenstellen. We nemen twee signalen met frequenties van 440 en 550 Hz. Samen vormen ze een grote terts: \[\begin{aligned} s_1(t) &= \sin(2\pi\cdot 440\cdot t)\\ \\ s_2(t) &= \sin(2\pi\cdot 550\cdot t)\\ \\ s(t) &= s_1(t)+s_2(t)=\sin(2\pi\cdot 440\cdot t)+\sin(2\pi\cdot 550\cdot t)\end{aligned}\]
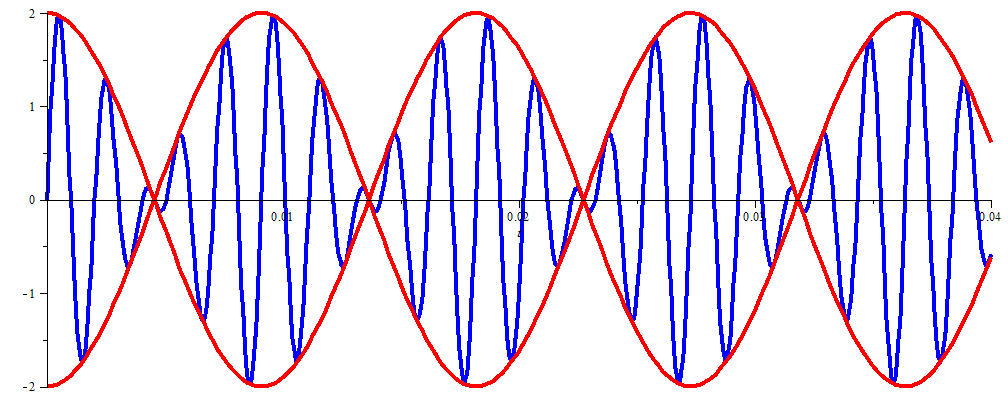
De grafiek van het somsignaal \(s(t)\) is hieronder te zien. De formule kan herschreven worden als \[s(t)=2\sin(2\pi\cdot 495\cdot t)\cdot \cos(2\pi\cdot 55\cdot t)\] In onderstaand diagram zijn ook de signalen \(\pm\cos(2\pi\cdot 55\cdot t)\) getekend.
Dit verklaart waarom men bij tegelijkertijd met de samenstellende tonen van 440 Hz en 550 Hz ook (zwak) de 'grondtoon' van 110 Hz kan horen: er zijn honderd en tien 'intensiteits'-toppen per seconde. Minder harmonieus klinkt de zweving die men hoort wanneer men twee ongeveer even sterke geluidssignalen samenstelt met frequenties die slechts weinig van elkaar verschillen. Een relatief langzame trilling kan duidelijk waargenomen worden.
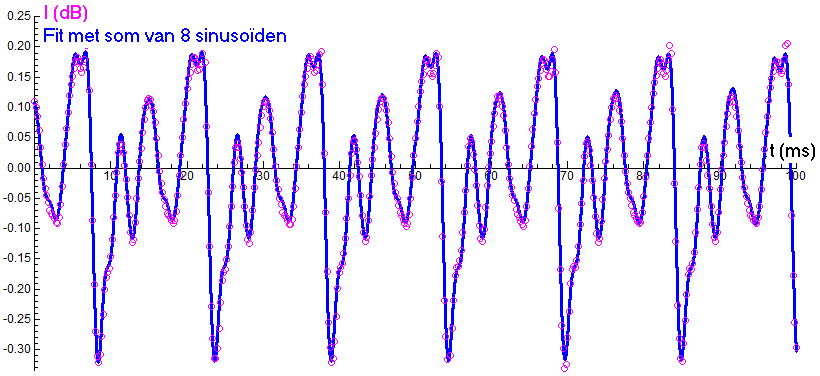
Klanken uit muziekinstrumenten zijn meestal samengesteld uit meer dan twee frequenties. Hieronder staat de meting van een lage klank op een baritonsaxofoon samen met de goede beschrijving van het signaal met 8 sinusoïden. Het frequentie-amplitudespectrum van het signaal is weergegeven als staafdiagram. De gemeten frequenties zijn gehele veelvouden van de grondtoon C2 (65.406 Hz).
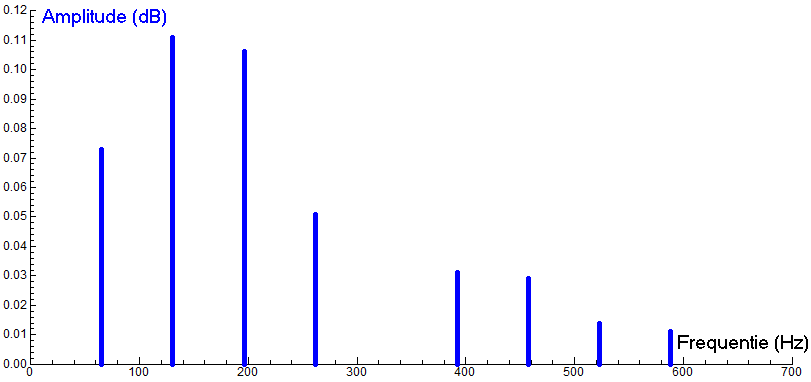
Het voorlaatste voorbeeld is een toepassing in de spraakherkenning, waar verschillende klinkers duidelijk verschillende patronen van intensiteiten voor het frequentiespectrum hebben. De frequenties met de hoogste intensiteiten heten formanten en bijvoorbeeld de afstand tussen de twee of drie laagste formanten is een belangrijk kenmerk om klinkers te onderscheiden.
Hieronder staat de grafiek van de korte geluidsmeting van de uitgesproken klinker 'ee' (als in 'beet') samen met de goede beschrijving van het signaal met 4 sinusoïden. Uit het frequentie-amplitudespectrum (niet getoond) blijkt dat de tweede formant een drievoud van de eerste formant is.
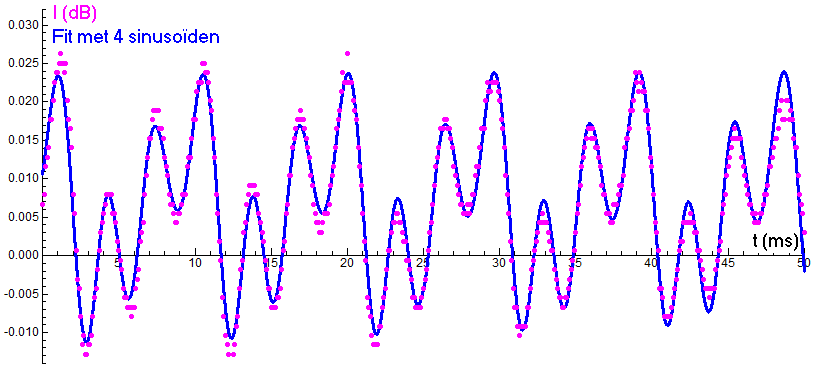
Het laatste voorbeeld komt uit de analyse van elektro-encefalografische (EEG) signalen. Dit zijn registraties via de hoofdhuid van veranderingen in elektrische potentiaalverschillen in de hersenen. In EEG-spectraalanalyse wordt het biosignaal opgesplitst in bijdragen van talloze sinusoïden; in het vermogensspectrum is af te lezen welke frequenties het meest bijdragen. Dit spectrum wordt via computeranalyse van het gemeten EEG-signaal gegenereerd. In onderstaande figuur (Figuur 2.6B uit Purves et al., Principles of Cognitive Neuroscience, 2nd edition, 2013) is een EEG signaal van een normaal persoon die zijn ogen dicht houdt te zien samen met het vermogensspectrum. De frequenties die het meest dominant in het signaal aanwezig zijn liggen rondom 10 Hz, d.w.z. liggen in de zogenaamde alpha frequentieband (8 tot 14 Hz).
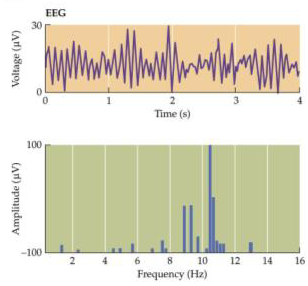
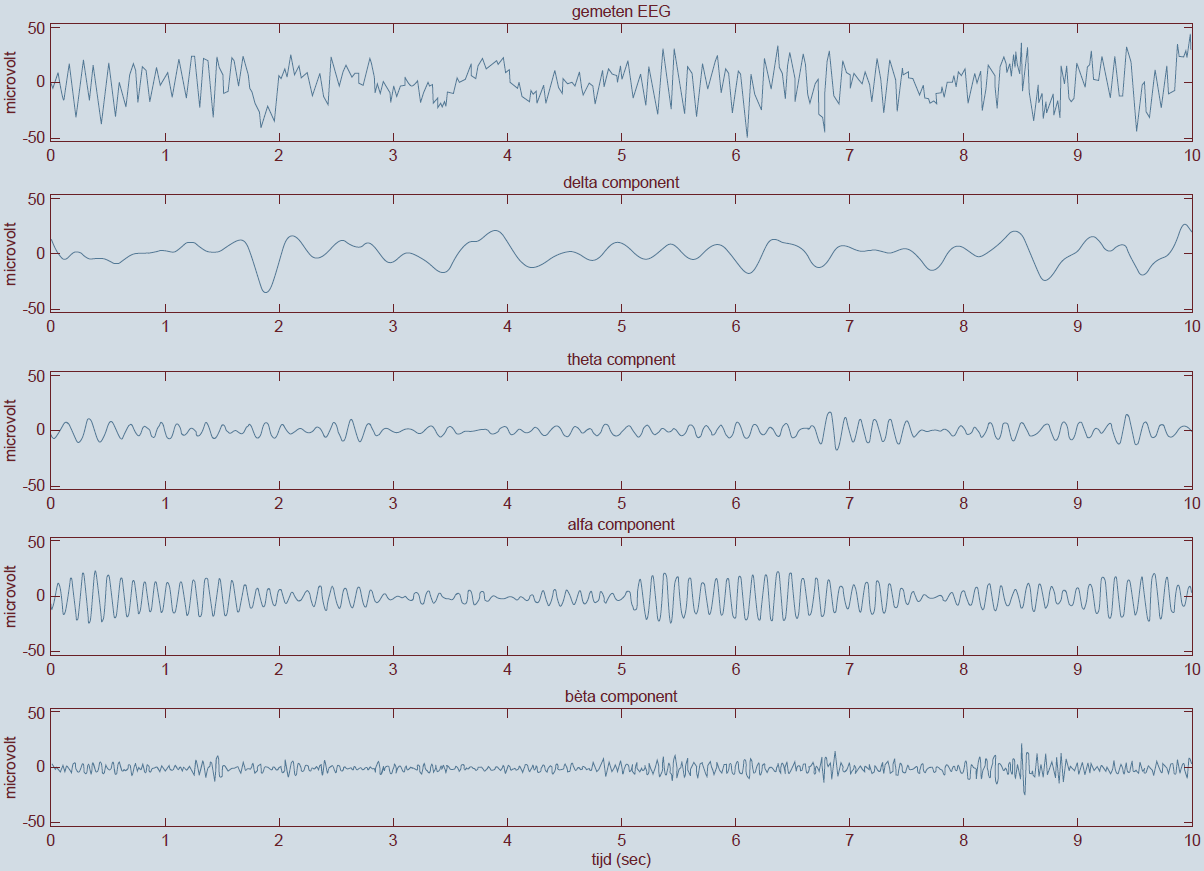
In EEG-spectraalanalyse wordt het signaal opgesplitst in bijdragen uit verschillende frequentiegebieden. In onderstaande figuur staat een episode van 10 seconden van een EEG-signaal in de bovenste grafiek. Dit signaal is met computeranalyse ontleed in deelsignalen waar alleen langzame frequenties (delta; 0 tot 4 Hz, 2e grafiek van boven), minder langzame (theta, 4 tot 8 Hz), snelle (alpha, 8 tot 12 Hz), snellere (SMR, 12 tot 14 Hz en bèta, 14 tot 38 Hz ) en snelste fluctuaties (gamma, 38 to 80 Hz) optreden. De optelsom van de vier onderste grafieken levert weer exact het oorspronkelijke signaal uit de bovenste grafiek op. Het uiterlijk van deze grafieken samen kan informatie geven over de staat waarin de hersenen zich bevinden, bijvoorbeeld of men slaapt, opgewonden of juist ontspannen is. Wanneer men in de klinische praktijk de uitspraak “we zien theta-activiteit” doet, dan bedoelt men feitelijk: “we zien een dominante theta-component”. In een echt EEG-signaal zitten ook altijd alpha-, bèta- en deltacomponenten! Gamma-golven hebben te maken met een sterke mentale activiteit zoals waarneming, oplossen van problemen, angst en bewustzijn.